
分析 (1)利用函數有意義,列出不等式組求解即可.
(2)利用函數的零點求出a,通過函數的對稱軸,求解函數的值域即可.
解答 解:(1)要使函數有意義,必須:$\left\{\begin{array}{l}{lo{g}_{2}x≥0}\\{16-{4}^{x-1}≥0}\end{array}\right.$,解得1≤x≤3,函數的定義域為:[1,3].
(2)函數g(x)=x2+ax+b的零點為-1,5,可得a=-(-1+5)=-4,b=-1×5=-5,
g(x)=x2-4x-5=(x-2)2-9,當x∈A時,即x∈[1,3]時,x=2函數取得最小值:y=-9,x=1或3時,函數取得最大值:-8.
函數g(x)的值域[-9,-8].
點評 本題考查函數的定義域的求法,二次函數的性質的應用,函數的零點的求法,考查計算能力.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2016 | B. | -2016 | C. | 1008 | D. | -1008 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | c>b>a | B. | c>a>b | C. | a>c>b | D. | a>b>c |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
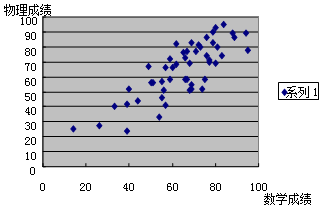 在調查分析某班級數學成績與物理成績的相關關系時,對數據進行統計分析得到如下散點圖,用回歸直線$\hat y=bx+a$近似刻畫其關系,根據圖形,b的數值最有可能是( )
在調查分析某班級數學成績與物理成績的相關關系時,對數據進行統計分析得到如下散點圖,用回歸直線$\hat y=bx+a$近似刻畫其關系,根據圖形,b的數值最有可能是( )| A. | 0 | B. | 1.55 | C. | 0.45 | D. | -0.24 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四邊形BFED是以BD為直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD.
如圖,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四邊形BFED是以BD為直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com