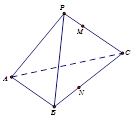
正三棱錐P—ABC中,CM=2PM,CN=2NB,對于以下結(jié)論:
①二面角B—PA—C大小的取值范圍是(
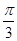
,π);
②若MN⊥AM,則PC與平面PAB所成角的大小為
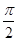
;
③過點M與異面直線PA和BC都成
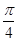
的直線有3條;
④若二面角B—PA—C大小為
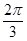
,則過點N與平面PAC和平面PAB都成
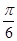
的直線有3條.
正確的序號是
.
試題分析:根據(jù)題意,由于正三棱錐P—ABC中,CM=2PM,CN=2NB,那么對于①二面角B—PA—C大小的取值范圍是(
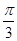
,π);成立。
②若MN⊥AM,則PC與平面PAB所成角的大小為
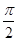
;成立
③過點M與異面直線PA和BC都成
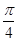
的直線有3條;不成立
④若二面角B—PA—C大小為
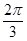
,則過點N與平面PAC和平面PAB都成
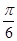
的直線有3條,成立,故填寫①②④
點評:利用線面角和二面角的平面角的定義,以及異面直線的所成的角的概念,進行求解確定,屬于基礎(chǔ)題。
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,在長方體
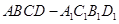
中,已知上下兩底面為正方形,且邊長均為1;側(cè)棱
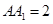
,
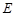
為

中點,
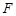
為
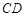
中點,
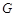
為
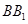
上一個動點.
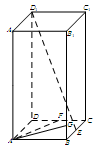
(Ⅰ)確定
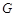
點的位置,使得

;
(Ⅱ)當(dāng)

時,求二面角
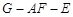
的平面角余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
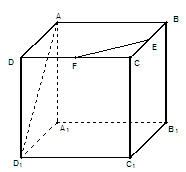
如圖,在棱長為
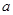
的正方體
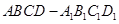
中,
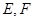
分別是
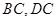
的中點,則異面直線
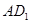
與
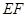
所成角等于
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,在長方體

中,

點

在棱

上.

(1)求異面直線

與

所成的角;
(2)若二面角

的大小為

,求點

到面

的距離.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
若
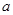
、
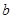
是直線,
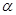
、
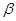
是平面,
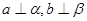
,向量
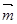
在
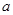
上,向量
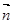
在
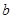
上,
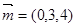
,
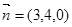
,則
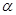
、
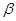
所成二面角中較小的一個余弦值為
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
正方體

中,二面角

的余弦值為
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
正方形ABCD所在平面與正方形ABEF所在平面成60°的二面角,則對角線AC與對角線BF對所成角的余弦值是__________. .
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知直線

與平面

所成的角為30°,

為空間一定點,過

作與

、

所成的角都是45°的直線

,則這樣的直線

可作( )條
查看答案和解析>>


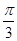 ,π);
,π);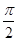 ;
;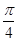 的直線有3條;
的直線有3條;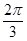 ,則過點N與平面PAC和平面PAB都成
,則過點N與平面PAC和平面PAB都成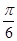 的直線有3條.
的直線有3條.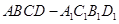 中,已知上下兩底面為正方形,且邊長均為1;側(cè)棱
中,已知上下兩底面為正方形,且邊長均為1;側(cè)棱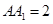 ,
,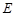 為
為 中點,
中點,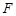 為
為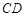 中點,
中點,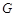 為
為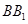 上一個動點.
上一個動點.
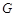 點的位置,使得
點的位置,使得 ;
; 時,求二面角
時,求二面角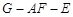 的平面角余弦值.
的平面角余弦值. 與平面
與平面 所成的角為30°,
所成的角為30°, 為空間一定點,過
為空間一定點,過 作與
作與 、
、 所成的角都是45°的直線
所成的角都是45°的直線 ,則這樣的直線
,則這樣的直線 可作( )條
可作( )條