
分析 (1)利用數學歸納法的證明步驟,證明求解即可.
(2)構造函數f(n)=a2n-an,判斷函數的單調性,轉化不等式為,對數不等式,通過函數的性質,轉化求解即可.
解答 (1)證:①當n=2時,左邊=${a_4}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}=\frac{25}{12}$,
右邊=$\frac{4}{2}=2$,左邊>右邊,命題成立;
②假設n=k時命題成立,即:${a_{2^k}}=1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2^k}>\frac{k+2}{2}$;
那么n=k+1時,${a_{{2^{k+1}}}}=1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2^k}+\frac{1}{{{2^k}+1}}+\frac{1}{{{2^k}+2}}+…+\frac{1}{{{2^{k+1}}}}$$>\frac{k+2}{2}+\frac{1}{{{2^k}+1}}+\frac{1}{{{2^k}+2}}+…+\frac{1}{{{2^{k+1}}}}$$>\frac{k+2}{2}+\frac{1}{{{2^{k+1}}}}+\frac{1}{{{2^{k+1}}}}+…+\frac{1}{{{2^{k+1}}}}$=$\frac{k+2}{2}+\frac{1}{2}$
=$\frac{(k+1)+2}{2}$
∴n=k+1時命題成立,
∴對于n≥2,n∈N*命題都成立.
(2)令f(n)=a2n-an=$\frac{1}{n+1}+\frac{1}{n+2}+\frac{1}{n+3}+…+\frac{1}{2n}$,
∴f(n+1)-f(n)=$\frac{1}{n+2}+\frac{1}{n+3}+…+\frac{1}{2n+2}$-($\frac{1}{n+1}+\frac{1}{n+2}+\frac{1}{n+3}+…+\frac{1}{2n}$)
=$\frac{1}{2n+1}+\frac{1}{2n+2}-\frac{1}{n+1}$=$\frac{1}{2n+1}-\frac{1}{2n+2}$>0,即f(n)單調遞增,
∴a2n-an≥f(2)=$\frac{7}{12}$,
故問題轉化為:$\frac{7}{12}$>$\frac{7}{12}$(loga+1x-logax+1)恒成立,
可得loga+1x<logax,即:lgx(lg(a+1)-lga)>0,可得x>1.
點評 本題考查是數學歸納法的應用,數列的函數的性質的應用,考查轉化思想以及計算能力.


 口算題天天練系列答案
口算題天天練系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
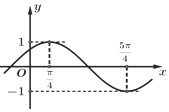 已知函數$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分圖象如圖所示.
已知函數$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分圖象如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com