
【題目】已知焦點在y軸上的橢圓E的中心是原點O,離心率等于![]() ,以橢圓E的長軸和短軸為對角線的四邊形的周長為
,以橢圓E的長軸和短軸為對角線的四邊形的周長為![]() .直線
.直線![]() 與
與![]() 軸交于點P,與橢圓E相交于A,B兩個點.
軸交于點P,與橢圓E相交于A,B兩個點.
(I)求橢圓E的方程;
(II)若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ) ![]() ;(Ⅱ)(1,4).
;(Ⅱ)(1,4).
【解析】試題分析:
(1)由題意求得a=2,b=1.∴橢圓E的方程為![]() +x2=1.
+x2=1.
(2)聯立直線與橢圓的方程,結合判別式為正數得到關于m的不等式,求解不等式可得![]() 的取值范圍是(1,4).
的取值范圍是(1,4).
試題解析:
(I)根據已知設橢圓E的方程為![]() +
+![]() =1(a>b>0),焦距為2c,
=1(a>b>0),焦距為2c,
由已知得![]() =
=![]() ,∴c=
,∴c=![]() a,b2=a2-c2=
a,b2=a2-c2=![]() .
.
∵以橢圓E的長軸和短軸為對角線的四邊形的周長為4![]() ,
,
∴4![]() =2
=2![]() a=4
a=4![]() ,∴a=2,b=1.∴橢圓E的方程為
,∴a=2,b=1.∴橢圓E的方程為![]() +x2=1.
+x2=1.
(II)根據已知得P(0,m),設A(x1,kx1+m),B(x2,kx2+m),
由![]() 得,(k2+4)x2+2mkx+m2-4=0.
得,(k2+4)x2+2mkx+m2-4=0.
由已知得Δ=4m2k2-4(k2+4)(m2-4)>0,即k2-m2+4>0,且x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
由![]() 得x1=-3x2.
得x1=-3x2.
∴3(x1+x2)2+4x1x2=12x-12x=0.
∴![]() +
+![]() =0,即m2k2+m2-k2-4=0.
=0,即m2k2+m2-k2-4=0.
當m2=1時,m2k2+m2-k2-4=0不成立,∴k2=![]() .
.
∵k2-m2+4>0,∴![]() -m2+4>0,即
-m2+4>0,即![]() >0.∴1<m2<4.
>0.∴1<m2<4.
∴m2的取值范圍為(1,4).


科目:高中數學 來源: 題型:
【題目】如圖,在正四棱錐![]() 中,O為頂點S在底面ABCD內的投影,P為側棱SD的中點,且
中,O為頂點S在底面ABCD內的投影,P為側棱SD的中點,且![]() .
.
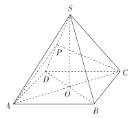
(1)證明:![]() 平面PAC.
平面PAC.
(2)求直線BC與平面PAC的所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
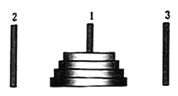
【題目】如圖所示,有三根針和套在一根針上的![]() 個金屬片,按下列規則,把金屬片從一根針上全部移到另一根針上.
個金屬片,按下列規則,把金屬片從一根針上全部移到另一根針上.
(1)每次只能移動一個金屬片;
(2)在每次移動過程中,每根針上較大的金屬片不能放在較小的金屬片上面.
將![]() 個金屬片從1號針移到3號針最少需要移動的次數記為
個金屬片從1號針移到3號針最少需要移動的次數記為![]() ,則
,則![]() __________.
__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從分別寫有數字1,2,3,4,5的5張卡片中隨機抽取1張,放回后再隨機抽取1張,則抽得的第一張卡片上的數字不大于第二張卡片的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在空間四邊形ABCD中,H,G分別是AD,CD的中點,E,F分別邊AB,BC上的點,且![]() ;
;

求證:(1)點E,F,G,H四點共面;
(2)直線EH,BD,FG相交于同一點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一年級開設了豐富多彩的校本課程,現從甲、乙兩個班隨機抽取了5名學生校本課程的學分,統計如下表.
甲 | 8 | 11 | 14 | 15 | 22 |
乙 | 6 | 7 | 10 | 23 | 24 |
用![]() 分別表示甲、乙兩班抽取的5名學生學分的方差,計算兩個班學分的方差.得
分別表示甲、乙兩班抽取的5名學生學分的方差,計算兩個班學分的方差.得![]() ______,并由此可判斷成績更穩定的班級是______班.
______,并由此可判斷成績更穩定的班級是______班.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() ,
,![]() 是長軸的一個端點,弦
是長軸的一個端點,弦![]() 過橢圓的中心
過橢圓的中心![]() ,且
,且![]() .
.

(1)求橢圓![]() 的方程.
的方程.
(2)過橢圓![]() 右焦點
右焦點![]() 的直線,交橢圓
的直線,交橢圓![]() 于
于![]() 兩點,交直線
兩點,交直線![]() 于點
于點![]() ,判定直線
,判定直線![]() 的斜率是否依次構成等差數列?請說明理由.
的斜率是否依次構成等差數列?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某蔬菜批發商分別在甲、乙兩市場銷售某種蔬菜(兩個市場的銷售互不影響),己知該蔬菜每售出1噸獲利500元,未售出的蔬菜低價處理,每噸虧損100 元.現統計甲、乙兩市場以往100個銷售周期該蔬菜的市場需求量的頻數分布,如下表:
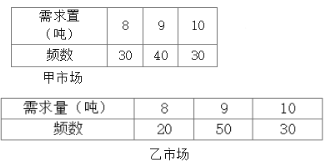
以市場需求量的頻率代替需求量的概率.設批發商在下個銷售周期購進![]() 噸該蔬菜,在 甲、乙兩市場同時銷售,以
噸該蔬菜,在 甲、乙兩市場同時銷售,以![]() (單位:噸)表示下個銷售周期兩市場的需求量,
(單位:噸)表示下個銷售周期兩市場的需求量,![]() (單位:元)表示下個銷售周期兩市場的銷售總利潤.
(單位:元)表示下個銷售周期兩市場的銷售總利潤.
(Ⅰ)當![]() 時,求
時,求![]() 與
與![]() 的函數解析式,并估計銷售利潤不少于8900元的槪率;
的函數解析式,并估計銷售利潤不少于8900元的槪率;
(Ⅱ)以銷售利潤的期望為決策依據,判斷![]() 與
與![]() 應選用哪—個.
應選用哪—個.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com