
【題目】某基地蔬菜大棚采用水培、無土栽培方式種植各類蔬菜.過去50周的資料顯示,該地周光照量![]() (小時)都在30小時以上,其中不足50小時的周數有5周,不低于50小時且不超過70小時的周數有35周,超過70小時的周數有10周.根據統計,該基地的西紅柿增加量
(小時)都在30小時以上,其中不足50小時的周數有5周,不低于50小時且不超過70小時的周數有35周,超過70小時的周數有10周.根據統計,該基地的西紅柿增加量![]() (百斤)與使用某種液體肥料
(百斤)與使用某種液體肥料![]() (千克)之間對應數據為如圖所示的折線圖.
(千克)之間對應數據為如圖所示的折線圖.
(1)依據數據的折線圖,是否可用線性回歸模型擬合![]() 與
與![]() 的關系?請計算相關系數
的關系?請計算相關系數![]() 并加以說明(精確到0.01).(若
并加以說明(精確到0.01).(若![]() ,則線性相關程度很高,可用線性回歸模型擬合)
,則線性相關程度很高,可用線性回歸模型擬合)
(2)蔬菜大棚對光照要求較大,某光照控制儀商家為該基地提供了部分光照控制儀,但每周光照控制儀最多可運行臺數受周光照量![]() 限制,并有如下關系:
限制,并有如下關系:
周光照量 |
|
|
|
光照控制儀最多可運行臺數 | 3 | 2 | 1 |
若某臺光照控制儀運行,則該臺光照控制儀周利潤為3000元;若某臺光照控制儀未運行,則該臺光照控制儀周虧損1000元.若商家安裝了3臺光照控制儀,求商家在過去50周周總利潤的平均值.

附:相關系數公式 ,參考數據
,參考數據![]() ,
,![]() .
.
【答案】(1)見解析.(2)商家在過去50周周總利潤的平均值為4600元.
【解析】分析:(1)由題中所給的數據求得線性回歸方程,然后進行預測即可;
(2)由題意分類討論X的范圍,求解即可.
詳解:(1)由已知數據可得![]() ,
,![]() .
.
因為![]()
![]()
![]()
所以相關系數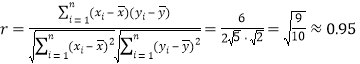 .
.
因為![]() ,所以可用線性回歸模型擬合
,所以可用線性回歸模型擬合![]() 與
與![]() 的關系.
的關系.
(2)記商家周總利潤為![]() 元,由條件可得在過去50周里:
元,由條件可得在過去50周里:
當![]() 時,共有10周,此時只有1臺光照控制儀運行,周總利潤
時,共有10周,此時只有1臺光照控制儀運行,周總利潤![]() =1×3000-2×1000=1000元
=1×3000-2×1000=1000元
當![]() 時,共有35周,此時2臺光照控制儀運行,周總利潤
時,共有35周,此時2臺光照控制儀運行,周總利潤![]() =2×3000-1×1000=5000元.
=2×3000-1×1000=5000元.
當![]() 時,共有5周,此時3臺光照控制儀都運行,周總利潤
時,共有5周,此時3臺光照控制儀都運行,周總利潤![]() =3×3000=9000元.
=3×3000=9000元.
所以過去50周周總利潤的平均值![]() 元,
元,
所以商家在過去50周周總利潤的平均值為4600元.


 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南師范大學出版社系列答案
同步練習西南師范大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐V-ABC中,平面VAB![]() 平面ABC,
平面ABC, ![]() VAB為等邊三角形,AC
VAB為等邊三角形,AC![]() BC且AC=BC=
BC且AC=BC=![]() ,O,M分別為AB,VA的中點。
,O,M分別為AB,VA的中點。
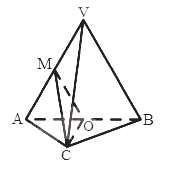
(I)求證:VB//平面MOC;
(II)求證:平面MOC![]() 平面VAB;
平面VAB;
(III)求三棱錐V-ABC的體積。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓錐曲線![]() 的方程為
的方程為![]() .
.
(![]() )在所給坐標系中畫出圓錐曲線
)在所給坐標系中畫出圓錐曲線![]() .
.
(![]() )圓錐曲線
)圓錐曲線![]() 的離心率
的離心率![]() __________.
__________.
(![]() )如果頂點在原點的拋物線
)如果頂點在原點的拋物線![]() 與圓錐曲線
與圓錐曲線![]() 有一個公共焦點
有一個公共焦點![]() ,且過第一象限,則
,且過第一象限,則
(i)交點![]() 的坐標為__________.
的坐標為__________.
(ii)拋物線![]() 的方程為__________.
的方程為__________.
(iii)在圖中畫出拋物線![]() 的準線.
的準線.
(![]() )已知矩形
)已知矩形![]() 各頂點都在圓錐曲線
各頂點都在圓錐曲線![]() 上,則矩形
上,則矩形![]() 面積的最大值為__________.
面積的最大值為__________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,圓心為
,圓心為![]() ,定點
,定點![]() ,
, ![]() 為圓
為圓![]() 上一點,線段
上一點,線段![]() 上一點
上一點![]() 滿足
滿足![]() ,直線
,直線![]() 上一點
上一點![]() ,滿足
,滿足![]() .
.
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)![]() 為坐標原點,
為坐標原點, ![]() 是以
是以![]() 為直徑的圓,直線
為直徑的圓,直線![]() 與
與![]() 相切,并與軌跡
相切,并與軌跡![]() 交于不同的兩點
交于不同的兩點![]() .當
.當![]() 且滿足
且滿足![]() 時,求
時,求![]() 面積
面積![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐![]() 中,四邊形
中,四邊形![]() 為矩形,
為矩形, ![]() 為等腰三角形,
為等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點.
的中點.

(1)證明: ![]() 平面
平面![]() ;
;
(2)證明:平面![]() 平面
平面![]() ;
;
(3)求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若直線![]() 和
和![]() 是異面直線,
是異面直線,![]() 在平面
在平面![]() 內,
內,![]() 在平面
在平面![]() 內,
內,![]() 是平面
是平面![]() 與平面
與平面![]() 的交線,則下列結論正確的是( )
的交線,則下列結論正確的是( )
A. ![]() 至少與
至少與![]() ,
,![]() 中的一條相交 B.
中的一條相交 B. ![]() 與
與![]() ,
,![]() 都不相交
都不相交
C. ![]() 與
與![]() ,
,![]() 都相交 D.
都相交 D. ![]() 至多與
至多與![]() ,
,![]() 中的一條相交
中的一條相交
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過拋物線![]() 的焦點
的焦點![]() ,斜率為
,斜率為![]() 的直線交拋物線于
的直線交拋物線于![]() 兩點,且
兩點,且![]() .
.
(1)求該拋物線![]() 的方程;
的方程;
(2)已知拋物線上一點![]() ,過點
,過點![]() 作拋物線的兩條弦
作拋物線的兩條弦![]() 和
和![]() ,且
,且![]() ,判斷直線
,判斷直線![]() 是否過定點?并說明理由.
是否過定點?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業里工人的工資與其生產利潤滿足線性相關關系,現統計了100名工人的工資![]() (元)與其生產利潤
(元)與其生產利潤![]() (千元)的數據,建立了
(千元)的數據,建立了![]() 關于
關于![]() 的回歸直線方程為
的回歸直線方程為![]() ,則下列說法正確的是( )
,則下列說法正確的是( )
A. 工人甲的生產利潤為1000元,則甲的工資為130元
B. 生產利潤提高1000元,則預計工資約提高80元
C. 生產利潤提高1000元,則預計工資約提高130元
D. 工人乙的工資為210元,則乙的生產利潤為2000元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中點,
的中點, ![]() 是
是![]() 與
與![]() 的交點,將
的交點,將![]() 沿
沿![]() 折起到
折起到![]() 的位置,如圖2.
的位置,如圖2.
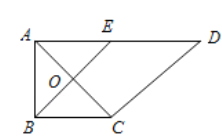

圖1 圖2
(1)證明: ![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com