
【題目】如圖所示,在四棱錐![]() 中,四邊形
中,四邊形![]() 為矩形,
為矩形, ![]() 為等腰三角形,
為等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點.
的中點.

(1)證明: ![]() 平面
平面![]() ;
;
(2)證明:平面![]() 平面
平面![]() ;
;
(3)求四棱錐![]() 的體積.
的體積.
【答案】(1)見解析;(2) 見解析;(3)![]() .
.
【解析】試題分析:(1)EF∥平面PAD,根據直線與平面平行的判定定理可知只需證EF與平面PAD內一直線平行,連AC,根據中位線可知EF∥PA,EF平面PAD,PA平面PAD,滿足定理所需條件;
(2平面PAD⊥平面ABCD,根據面面垂直的判定定理可知在平面ABCD內一直線與平面PAD垂直,根據面面垂直的性質定理可知CD⊥平面PAD,又CD平面ABCD,滿足定理所需條件;
(3)過P作PO⊥AD于O,從而PO⊥平面ABCD,即為四棱錐的高,最后根據棱錐的體積公式求出所求即可.
解:(1)如圖所示,
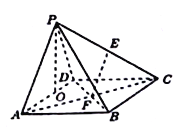
連接![]() . ∵四邊形
. ∵四邊形![]() 為矩形,且
為矩形,且![]() 為
為![]() 的中點,
的中點,
∴![]() 也是
也是![]() 的中點. 又
的中點. 又![]() 是
是![]() 的中點,
的中點, ![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .
.![]() 平面
平面![]()
(2) 證明:∵平面![]() 平面
平面![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() . ∵
. ∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(3)取![]() 的中點
的中點![]() ,連接
,連接![]() . ∵平面
. ∵平面![]() 平面
平面![]() ,
, ![]() 為等腰三角形,
為等腰三角形,
∴![]() 平面
平面![]() ,即
,即![]() 為四棱錐
為四棱錐![]() 的高. ∵
的高. ∵![]() ,∴
,∴![]() . 又
. 又![]() ,
,
∴四棱錐![]() 的體積
的體積![]() .
.


科目:高中數學 來源: 題型:
【題目】(改編)已知正數數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ;在數列
;在數列![]() 中,
中,![]()
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)設![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() . 若對任意
. 若對任意![]() ,存在實數
,存在實數![]() ,使
,使![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(3)記數列![]() 的前
的前![]() 項和為
項和為![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]()
(1)若直線![]() 與圓
與圓![]() 相交于兩點
相交于兩點![]() ,弦長
,弦長![]() 等于
等于![]() ,求
,求![]() 的值;
的值;
(2)已知點![]() ,點
,點![]() 為圓心,若在直線
為圓心,若在直線![]() 上存在定點
上存在定點![]() (異于點
(異于點![]() ),滿足:對于圓
),滿足:對于圓![]() 上任一點
上任一點![]() ,都有
,都有![]() 為一常數,試求所有滿足條件的點
為一常數,試求所有滿足條件的點![]() 的坐標及改常數.
的坐標及改常數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校高一數學考試后,對![]() 分(含
分(含![]() 分)以上的成績進行統計,其頻率分布直方圖如圖所示,分數在
分)以上的成績進行統計,其頻率分布直方圖如圖所示,分數在![]() 分的學生人數為
分的學生人數為![]() 人,
人,

(1)求這所學校分數在![]() 分的學生人數;
分的學生人數;
(2)請根據頻率發布直方圖估計這所學校學生分數在![]() 分的學生的平均成績;
分的學生的平均成績;
(3)為進“步了解學生的學習情況,按分層抽樣方法從分數在![]() 分和
分和![]() 分的學生中抽出
分的學生中抽出![]() 人,從抽出的學生中選出
人,從抽出的學生中選出![]() 人分別做問卷
人分別做問卷![]() 和問卷
和問卷![]() ,求
,求![]() 分的學生做問卷
分的學生做問卷![]() ,
,![]() 分的學生做問卷
分的學生做問卷![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某基地蔬菜大棚采用水培、無土栽培方式種植各類蔬菜.過去50周的資料顯示,該地周光照量![]() (小時)都在30小時以上,其中不足50小時的周數有5周,不低于50小時且不超過70小時的周數有35周,超過70小時的周數有10周.根據統計,該基地的西紅柿增加量
(小時)都在30小時以上,其中不足50小時的周數有5周,不低于50小時且不超過70小時的周數有35周,超過70小時的周數有10周.根據統計,該基地的西紅柿增加量![]() (百斤)與使用某種液體肥料
(百斤)與使用某種液體肥料![]() (千克)之間對應數據為如圖所示的折線圖.
(千克)之間對應數據為如圖所示的折線圖.
(1)依據數據的折線圖,是否可用線性回歸模型擬合![]() 與
與![]() 的關系?請計算相關系數
的關系?請計算相關系數![]() 并加以說明(精確到0.01).(若
并加以說明(精確到0.01).(若![]() ,則線性相關程度很高,可用線性回歸模型擬合)
,則線性相關程度很高,可用線性回歸模型擬合)
(2)蔬菜大棚對光照要求較大,某光照控制儀商家為該基地提供了部分光照控制儀,但每周光照控制儀最多可運行臺數受周光照量![]() 限制,并有如下關系:
限制,并有如下關系:
周光照量 |
|
|
|
光照控制儀最多可運行臺數 | 3 | 2 | 1 |
若某臺光照控制儀運行,則該臺光照控制儀周利潤為3000元;若某臺光照控制儀未運行,則該臺光照控制儀周虧損1000元.若商家安裝了3臺光照控制儀,求商家在過去50周周總利潤的平均值.

附:相關系數公式 ,參考數據
,參考數據![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知n為正整數,數列{an}滿足an>0,4(n+1)an2﹣nan+12=0,設數列{bn}滿足bn= ![]()
(1)求證:數列{ ![]() }為等比數列;
}為等比數列;
(2)若數列{bn}是等差數列,求實數t的值:
(3)若數列{bn}是等差數列,前n項和為Sn , 對任意的n∈N* , 均存在m∈N* , 使得8a12Sn﹣a14n2=16bm成立,求滿足條件的所有整數a1的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() ,
,![]() 時,求滿足
時,求滿足![]() 的
的![]() 的值;
的值;
(2)若函數![]() 是定義在
是定義在![]() 上的奇函數.
上的奇函數.
①存在![]() ,使得不等式
,使得不等式![]() 有解,求實數
有解,求實數![]() 的取值范圍;
的取值范圍;
②若函數![]() 滿足
滿足![]() ,若對任意
,若對任意![]() 且
且![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代著名數學經典.其中對勾股定理的論術比西方早一千多年,其中有這樣一個問題:“今有圓材埋在壁中,不知大小.以鋸鋸之,深一寸,鋸道長一尺.問徑幾何?”其意為:今有一圓柱形木材,埋在墻壁中,不知其大小,用鋸去鋸該材料,鋸口深1寸,鋸道長1尺.問這塊圓柱形木料的直徑是多少?長為1丈的圓柱形木材部分鑲嵌在墻體中,截面圖如圖所示(陰影部分為鑲嵌在墻體內的部分).已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算該木材鑲嵌在墻中的體積約為( )
寸,估算該木材鑲嵌在墻中的體積約為( )
(注:1丈=10尺=100寸, ![]() ,
, ![]() )
)

A. 633立方寸 B. 620立方寸 C. 610立方寸 D. 600立方寸
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com