
【題目】已知函數![]() ,
,![]() 在一個周期內的圖像如圖所示.
在一個周期內的圖像如圖所示.
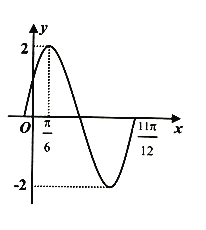
(I)求函數![]() 的解析式;
的解析式;
(II)設![]() ,且方程
,且方程![]() 有兩個不同的實數根,求實數
有兩個不同的實數根,求實數![]() 的取值范圍以及這兩個根的和.
的取值范圍以及這兩個根的和.
【答案】(Ⅰ)![]() .(Ⅱ)見解析.
.(Ⅱ)見解析.
【解析】
(I)根據三角函數的圖像的最高點,求得![]() 的值,根據三角函數的周期,求得
的值,根據三角函數的周期,求得![]() 的值,根據函數圖像上的特殊點,求得
的值,根據函數圖像上的特殊點,求得![]() 的值,由此求得函數的解析式.(II)畫出函數
的值,由此求得函數的解析式.(II)畫出函數![]() 的圖像與函數
的圖像與函數![]() 的圖像,根據圖像求得
的圖像,根據圖像求得![]() 的的取值范圍.根據對稱性求得兩根的和.
的的取值范圍.根據對稱性求得兩根的和.
(I)由題設圖象,易得![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以![]() .
.
因為函數![]() 的圖象經過點
的圖象經過點![]() ,
,
所以![]() ,即
,即![]() .
.
又因為![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
故所求函數![]() 的解析式為
的解析式為![]() .
.
(Ⅱ)由題意,知方程![]() 有兩個不同的實數根等價于函數
有兩個不同的實數根等價于函數![]() 的圖象與
的圖象與![]() 的圖象有兩個不同的交點.
的圖象有兩個不同的交點.
因為![]() ,
,
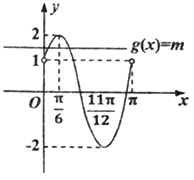
易畫出函數![]() 的圖象與函數
的圖象與函數![]() 的圖象(如圖所示).
的圖象(如圖所示).
依據圖象可知:
當![]() 或
或![]() 時,
時,
直線![]() 與曲線
與曲線![]() 有兩個不同的交點,
有兩個不同的交點,
即方程![]() 有兩個不同的實數根,
有兩個不同的實數根,
故所求實數![]() 的取值范圍為
的取值范圍為![]() .
.
①當![]() 時,
時,![]() 與
與![]() 的圖象有兩交點且關于直線
的圖象有兩交點且關于直線![]() 對稱,設此時方程
對稱,設此時方程![]() 兩個不同的實數根分別為
兩個不同的實數根分別為![]() ,
,![]() ,
,
所以當![]() ,即
,即![]()
②當![]() 時,
時,![]() 與
與![]() 的圖象有兩交點且關于直線
的圖象有兩交點且關于直線![]() 對稱,設此時方程
對稱,設此時方程![]() 兩個不同的實數根分別為
兩個不同的實數根分別為![]() ,
,![]() ,
,
所以![]() ,即
,即![]()
綜上,當![]() 時,所求方程的兩根之和為
時,所求方程的兩根之和為![]()
當![]() 時,所求方程的兩根之和為
時,所求方程的兩根之和為![]() .
.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:
【題目】某市一個社區微信群“步行者”有成員100人,其中男性70人,女性30人,現統計他們平均每天步行的時間,得到頻率分布直方圖,如圖所示:

若規定平均每天步行時間不少于2小時的成員為“步行健將”,低于2小時的成員為“非步行健將”.已知“步行健將”中女性占![]() .
.
(1)填寫下面![]() 列聯表,并通過計算判斷能否在犯錯誤的概率不超過0.05的前提下認為“是否為‘步行健將’與性別有關”;
列聯表,并通過計算判斷能否在犯錯誤的概率不超過0.05的前提下認為“是否為‘步行健將’與性別有關”;

(2)現從“步行健將”中隨機選派2人參加全市業余步行比賽,求2人中男性的人數![]() 的分布列及數學期望.
的分布列及數學期望.
參考公式:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體ABC—DEF中,若AB//DE,BC//EF.
(1)求證:平面ABC//平面DEF;
(2)已知![]() 是二面角C-AD-E的平面角.求證:平面ABC
是二面角C-AD-E的平面角.求證:平面ABC![]() 平面DABE.
平面DABE.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是中國古代第一部數學專著,成于公元一世紀左右,系統總結了戰國、秦、漢時期的數學成就.其中《方田》一章中記載了計算弧田(弧田就是由圓弧和其所對弦所圍成弓形)的面積所用的經驗公式:弧田面積=![]() (弦×矢+矢×矢),公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差.按照上述經驗公式計算所得弧田面積與其實際面積之間存在誤差.現有圓心角為
(弦×矢+矢×矢),公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差.按照上述經驗公式計算所得弧田面積與其實際面積之間存在誤差.現有圓心角為![]() ,弦長為
,弦長為![]() 的弧田.其實際面積與按照上述經驗公式計算出弧田的面積之間的誤差為( )平方米.(其中
的弧田.其實際面積與按照上述經驗公式計算出弧田的面積之間的誤差為( )平方米.(其中![]() ,
,![]() )
)
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某產品的廣告支出x(單位:萬元)與銷售收入y(單位:萬元)之間有下表所對應的數據:
廣告支出x(單位:萬元) | 1 | 2 | 3 | 4 |
銷售收入y(單位:萬元) | 12 | 28 | 42 | 56 |
(1)畫出表中數據的散點圖;
(2)求出y對x的回歸直線方程![]() ;
;
(3)若廣告費為9萬元,則銷售收入約為多少萬元?
參考公式: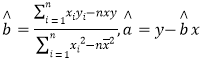
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為慶祝成立二十周年,特舉辦《快樂大闖關》競技類有獎活動,該活動共有四關,由兩名男職員與兩名女職員組成四人小組,設男職員闖過一至四關概率依次是![]() ,女職員闖過一至四關的概率依次是
,女職員闖過一至四關的概率依次是![]()
(1)求女職員闖過四關的概率;
(2)設![]() 表示四人小組闖過四關的人數,求隨機變量
表示四人小組闖過四關的人數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在十九大“建設美麗中國”的號召下,某省級生態農業示范縣大力實施綠色生產方案,對某種農產品的生產方式分別進行了甲、乙兩種方案的改良。為了檢查甲、乙兩種方案的改良效果,隨機在這兩種方案中各任意抽取了![]() 件產品作為樣本逐件稱出它們的重量(單位:克),重量值落在
件產品作為樣本逐件稱出它們的重量(單位:克),重量值落在![]() 之間的產品為合格品,否則為不合格品。下表是甲、乙兩種方案樣本頻數分布表。
之間的產品為合格品,否則為不合格品。下表是甲、乙兩種方案樣本頻數分布表。
產品重量 | 甲方案頻數 | 乙方案頻數 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求出甲(同組中的重量值用組中點值代替)方案樣本中![]() 件產品的平均數;
件產品的平均數;
(2)若以頻率作為概率,試估計從兩種方案分別任取![]() 件產品,恰好兩件產品都是合格品的概率分別是多少;
件產品,恰好兩件產品都是合格品的概率分別是多少;
(3)由以上統計數據完成下面![]() 列聯表,并回答有多大把握認為“產品是否為合格品與改良方案的選擇有關”.
列聯表,并回答有多大把握認為“產品是否為合格品與改良方案的選擇有關”.
甲方案 | 乙方案 | 合計 | |
合格品 | |||
不合格品 | |||
合計 |
參考公式: 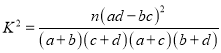 ,其中
,其中![]() .
.
臨界值表:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() +
+![]() =1(a>b>0)的焦點分別為F1(0,-1),F2(0,1),且3a2=4b2.
=1(a>b>0)的焦點分別為F1(0,-1),F2(0,1),且3a2=4b2.
(1)求橢圓的方程;
(2)設點P在這個橢圓上,且|PF1|-|PF2|=1,求∠F1PF2的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,等邊△ABC與直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M為AB的中點.
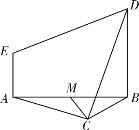
(1)證明:CM⊥DE;
(2)在邊AC上找一點N,使CD∥平面BEN.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com