
���}Ŀ����D����߅��ABC�cֱ������ABDE����ƽ�洹ֱ��BD��AE��BD��2AE��AE��AB��M��AB�����c(di��n)��
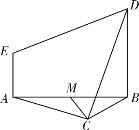
(1)�C����CM��DE��
(2)��߅AC����һ�c(di��n)N��ʹCD��ƽ��BEN.
���𰸡���1��Ҋ��������2��![]() ��
��![]() ߅�Ͽ���
߅�Ͽ���![]() �����ȷ��c(di��n)���C��Ҋ����.
�����ȷ��c(di��n)���C��Ҋ����.
��������
��1������(j��)��߅�������C��![]() ���ٸ���(j��)���洹ֱ�����|(zh��)�����õ����洹ֱ�����þ��洹ֱ�����|(zh��)�õ��Y(ji��)Փ����2��ȡ��
���ٸ���(j��)���洹ֱ�����|(zh��)�����õ����洹ֱ�����þ��洹ֱ�����|(zh��)�õ��Y(ji��)Փ����2��ȡ��![]() ����(d��ng)
����(d��ng)![]() �c
�c![]() ��һ�c(di��n)�B����(g��u)��ƽ��r(sh��)������(j��)����ƽ�����|(zh��)������֪������ƽ���c��
��һ�c(di��n)�B����(g��u)��ƽ��r(sh��)������(j��)����ƽ�����|(zh��)������֪������ƽ���c��![]() �Ľ�����ƽ����
�Ľ�����ƽ����![]() ����������һ��(g��)���c(di��n)
����������һ��(g��)���c(di��n)![]() ���tֻ���^
���tֻ���^![]() ��
��![]() ��ƽ�о����c
��ƽ�о����c![]() ���c(di��n)����
���c(di��n)����![]() ������(j��)�L���P(gu��n)ϵ��֪��
������(j��)�L���P(gu��n)ϵ��֪��![]() ��
��![]() ߅�Ͽ���
߅�Ͽ���![]() �����ȷ��c(di��n)��ͨ�^��
�����ȷ��c(di��n)��ͨ�^��![]() ���c(di��n)
���c(di��n)![]() ��
��![]() �����C��
�����C��![]() ��
��![]() ��
��![]() ���c(di��n)������(j��)ƽ�о��־��γɱ������L���P(gu��n)ϵ���C��
���c(di��n)������(j��)ƽ�о��־��γɱ������L���P(gu��n)ϵ���C��![]() ���Ķ��C��
���Ķ��C��![]() ����������������λ����
����������������λ����![]() ���Ķ���
���Ķ���![]() ������(j��)����ƽ���ж����������C�ýY(ji��)Փ����.
������(j��)����ƽ���ж����������C�ýY(ji��)Փ����.
��1��![]()
![]() ���߅�����Σ���
���߅�����Σ���![]() ��
��![]() ���c(di��n)
���c(di��n) ![]()
��ƽ��![]() ƽ��
ƽ��![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]()
![]() ƽ��
ƽ��![]()
��![]() ƽ��
ƽ��![]()
![]()
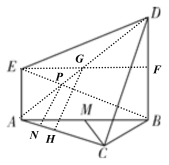
��2��![]() ��
��![]() ߅�Ͽ���
߅�Ͽ���![]() �����ȷ��c(di��n)���C�����£�
�����ȷ��c(di��n)���C�����£�
ȡ![]() ���c(di��n)
���c(di��n)![]() ���B��
���B��![]() ��
��![]() ��
��![]()
ȡ![]() ���c(di��n)
���c(di��n)![]() ���B��
���B�����B��
![]() ��
��![]() ��
��![]()
![]() ��
��![]() ��
��![]() ���c(di��n)��
���c(di��n)��![]()
![]()
![]() ��
��![]() ���c(di��n)
���c(di��n)
![]()
![]()
![]()
![]() ��
��![]() ߅�Ͽ���
߅�Ͽ���![]() �����ȷ��c(di��n)
�����ȷ��c(di��n)
��![]()
![]()
![]()
��![]()
![]()
��![]() �քe��
�քe��![]() ���c(di��n)
���c(di��n) ![]()
![]()
��![]() ��
��![]() ��
��![]() ��
��![]()
![]() ��
��![]()


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��һ��(g��)���ڃ�(n��i)�ĈD����D��ʾ.
��һ��(g��)���ڃ�(n��i)�ĈD����D��ʾ.
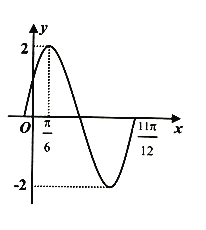
��I����(sh��)![]() �Ľ���ʽ��
�Ľ���ʽ��
��II���O(sh��)![]() ���ҷ���
���ҷ���![]() �Ѓɂ�(g��)��ͬ�Č�(sh��)��(sh��)������(sh��)��(sh��)
�Ѓɂ�(g��)��ͬ�Č�(sh��)��(sh��)������(sh��)��(sh��)![]() ��ȡֵ�����Լ��@�ɂ�(g��)���ĺ�.
��ȡֵ�����Լ��@�ɂ�(g��)���ĺ�.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���ʣ� ![]() ���У���sin��=
������sin��= ![]() ��
��
��1����sin�� ![]() +������ֵ��
+������ֵ��
��2����cos�� ![]() ��2������ֵ��
��2������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f (x)��ex��g(x)��x��b��b��R��
��1��������(sh��)f (x)�ĈD���c����(sh��)g(x)�ĈD�����У���b��ֵ��
��2���O(sh��)T(x)��f (x)��ag(x)��a��R����(sh��)T(x)���{(di��o)���^(q��)�g��
��3���O(sh��)h(x)��|g(x)|��f (x)��b��1��������x1��x2![]() [0��1]��ʹ|h(x1)��h(x2)|��1��������b��ȡֵ������
[0��1]��ʹ|h(x1)��h(x2)|��1��������b��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���o���E�AC��![]() (a��b��0)���Q�AC1��x2��y2��a2��b2��E�AC�������S�A������֪�E�AC���x���ʞ�
(a��b��0)���Q�AC1��x2��y2��a2��b2��E�AC�������S�A������֪�E�AC���x���ʞ�![]() ���ҽ�(j��ng)�^�c(di��n)(0��1)��
���ҽ�(j��ng)�^�c(di��n)(0��1)��
��1����(sh��)��(sh��)a��b��ֵ��
��2�����^�c(di��n)P(0��m)(m��0)��ֱ��l�c�E�AC����ֻ��һ��(g��)�����c(di��n)����l���E�AC�İ��S�AC1���صõ����L��2![]() ����(sh��)��(sh��)m��ֵ��
����(sh��)��(sh��)m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ס��ҡ���3��Ͷ�@,Ͷ�M(j��n)�ĸ��ʷքe��![]() .
.
(��)�F(xi��n)3�˸�Ͷ�@1��,��3�˶��]��Ͷ�M(j��n)�ĸ��ʣ�
(��)��![]() ��ʾ��Ͷ�@3�ε��M(j��n)��(sh��),���S�C(j��)׃��
��ʾ��Ͷ�@3�ε��M(j��n)��(sh��),���S�C(j��)׃��![]() �ĸ��ʷֲ�����(sh��)�W(xu��)����
�ĸ��ʷֲ�����(sh��)�W(xu��)����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ָͨ��(sh��)��ָ��ͨ����ָ��(sh��)�ĺ��Q���ǾC�Ϸ�ӳ��·�W(w��ng)��ͨ����µĸ�����ָ��(sh��)ֵ��ӛ��ָͨ��(sh��)��![]() ���䷶����
���䷶����![]() ���քe���傀(g��)���e��
���քe���傀(g��)���e��![]() ����ͨ��
����ͨ��![]() ��������ͨ��
��������ͨ��![]() ���p�ȓ��£�
���p�ȓ��£�![]() ���жȓ��£�
���жȓ��£�![]() ����(y��n)��?f��)��?�����߷�r(sh��)�Σ�
����(y��n)��?f��)��?�����߷�r(sh��)�Σ�![]() ������ij�н�ָͨ�]�����xȡ���Ѕ^(q��)20��(g��)��ͨ·�Σ�����(j��)�佻ָͨ��(sh��)��(sh��)��(j��)�L�Ƶ��l�ʷֲ�ֱ���D��D��ʾ.
������ij�н�ָͨ�]�����xȡ���Ѕ^(q��)20��(g��)��ͨ·�Σ�����(j��)�佻ָͨ��(sh��)��(sh��)��(j��)�L�Ƶ��l�ʷֲ�ֱ���D��D��ʾ.
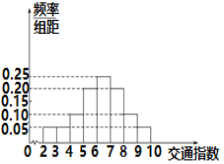
(1)����p�ȓ��¡��жȓ��¡���(y��n)��?f��)��µ�·�εĂ�(g��)��(sh��)��
(2)�÷ӳ�ӵķ������p�ȓ��¡��жȓ��¡���(y��n)��?f��)��µ�·���й����?��(g��)·�Σ������γ�ȡ������(g��)���e·�εĂ�(g��)��(sh��)��
(3)��(2)�г�ȡ��6��(g��)·������ȡ2��(g��)����������1��(g��)·�Ξ��p�ȓ��µĸ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��![]() ��Ȳ(sh��)�У�
��Ȳ(sh��)�У�![]() ��
��![]() .
.
��1�� ��(sh��)��![]() ��ͨ�(xi��ng)��ʽ;
��ͨ�(xi��ng)��ʽ;
��2����(sh��)��![]() ��ǰn�(xi��ng)��
��ǰn�(xi��ng)��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�^(q��)100λ������˾�����ˮ��(��λ��![]() )�ķֽM�����M���l��(sh��)���£�
)�ķֽM�����M���l��(sh��)���£�
![]() ��4��
��4�� ![]() ��8��
��8�� ![]() ��15��
��15��
![]() ��22��
��22�� ![]() ��25��
��25�� ![]() ��14��
��14��
![]() ��6��
��6�� ![]() ��4��
��4�� ![]() ��2��
��2��
(1)�г��ӱ����l�ʷֲ�����
(2)�����l�ʷֲ�ֱ���D��������(j��)ֱ���D��Ӌ(j��)�@�M��(sh��)��(j��)��ƽ����(sh��)����λ��(sh��)������(sh��)��
(3)��(d��ng)?sh��)������ƶ����˾�����ˮ���?/span>![]() �Ę�(bi��o)��(zh��n)����������(bi��o)��(zh��n)�ӱ����M(f��i)����(d��ng)?sh��)������f��
�Ę�(bi��o)��(zh��n)����������(bi��o)��(zh��n)�ӱ����M(f��i)����(d��ng)?sh��)������f��![]() ���ϵľ����^�@��(g��)��(bi��o)��(zh��n)���@��(g��)��ጌ����ʲô��
���ϵľ����^�@��(g��)��(bi��o)��(zh��n)���@��(g��)��ጌ����ʲô��
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com