
分析 由y=loga(x+1)+1在[0,+∞) 上遞減,得0<a<1,由f(x)在R上單調遞減,得a$≥\frac{1}{3}$,作出函數f(x)=$\left\{\begin{array}{l}{x^2}+3a,x<0\\{log_a}({x+1})+1,x≥0\end{array}$(a>0且a≠1)在R上的大致圖象,利用數形結合思想能求出a的取值范圍.
解答 解:由y=loga(x+1)+1在[0,+∞) 上遞減,得0<a<1,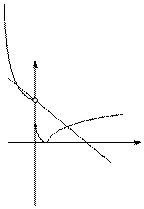
又由f(x)=$\left\{\begin{array}{l}{x^2}+3a,x<0\\{log_a}({x+1})+1,x≥0\end{array}$(a>0且a≠1)在R上單調遞減,
得02+3a≥f(0)=1,解得a$≥\frac{1}{3}$,
作出函數f(x)=$\left\{\begin{array}{l}{x^2}+3a,x<0\\{log_a}({x+1})+1,x≥0\end{array}$(a>0且a≠1)在R上的大致圖象,
由圖象可知,在[0,+∞) 上,|f(x)|=2-x 有且僅有一個解,
故在(-∞,0)上,|f(x)|=2-x 同樣有且僅有一個解,
當3a>2,即a>$\frac{2}{3}$ 時,聯立|x2+3a|=2-x,
則△=12-4(3a-2)=0,解得:$a=\frac{3}{4}$,
當1≤3a≤2 時,由圖象可知,符合條件.
綜上:a∈[$\frac{1}{3},\frac{2}{3}$]∪{$\frac{3}{4}$}.
故答案為:[$\frac{1}{3},\frac{2}{3}$]∪{$\frac{3}{4}$}.
點評 本題考查實數的取值范圍的求法,是中檔題,解題時要認真審題,注意函數性質及數形結合思想的合理運用.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [1,$\sqrt{2}$) | B. | (-$\sqrt{2}$,$\sqrt{2}$) | C. | (-$\sqrt{2}$,-1] | D. | [-1,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
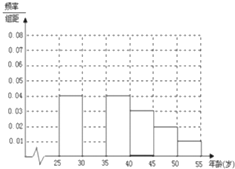 某班同學參加社會實踐活動,對本市25~55歲年齡段的人群進行某項隨機調查,得到各年齡段被調查人數的頻率分布直方圖如右(部分有缺損):
某班同學參加社會實踐活動,對本市25~55歲年齡段的人群進行某項隨機調查,得到各年齡段被調查人數的頻率分布直方圖如右(部分有缺損):查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com