
【題目】下列說法中,正確的個數是( )
(1)在頻率分布直方圖中,中位數左邊和右邊的直方圖的面積相等.
(2)如果一組數中每個數減去同一個非零常數,則這一組數的平均數改變,方差不改變.
(3)一個樣本的方差s2=![]() [(x
[(x![]() 一3)2+(X
一3)2+(X![]() —3)2+ +(X
—3)2+ +(X![]() 一3)2],則這組數據總和等于60.
一3)2],則這組數據總和等于60.
(4)數據![]() 的方差為
的方差為![]() ,則數據
,則數據![]() 的方差為
的方差為![]() .
.
A.4B.3C.2D.1
科目:高中數學 來源: 題型:
【題目】2019年初,某市為了實現教育資源公平,辦人民滿意的教育,準備在今年8月份的小升初錄取中在某重點中學實行分數和搖號相結合的錄取辦法.該市教育管理部門為了了解市民對該招生辦法的贊同情況,隨機采訪了440名市民,將他們的意見和是否近三年家里有小升初學生的情況進行了統計,得到如下的2×2列聯表.
贊同錄取辦法人數 | 不贊同錄取辦法人數 | 合計 | |
近三年家里沒有小升初學生 | 180 | 40 | 220 |
近三年家里有小升初學生 | 140 | 80 | 220 |
合計 | 320 | 120 | 440 |
(1)根據上面的列聯表判斷,能否在犯錯誤的概率不超過0.001的前提下認為是否贊同小升初錄取辦法與近三年是否家里有小升初學生有關;
(2)從上述調查的不贊同小升初錄取辦法人員中根據近三年家里是否有小升初學生按分層抽樣抽出6人,再從這6人中隨機抽出3人進行電話回訪,求3人中恰有1人近三年家里沒有小升初學生的概率.
附:![]() ,其中
,其中![]() .
.
P( | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從金山區走出去的陳馳博士,在《自然—可持續性》雜志上發表的論文中指出:地球正在變綠,中國通過植樹造林和提高農業效率,在其中起到了主導地位.已知某種樹木的高度![]() (單位:米)與生長年限
(單位:米)與生長年限![]() (單位:年,tN*)滿足如下的邏輯斯蒂函數:
(單位:年,tN*)滿足如下的邏輯斯蒂函數:![]() ,其中e為自然對數的底數. 設該樹栽下的時刻為0.
,其中e為自然對數的底數. 設該樹栽下的時刻為0. ![]()
(1)需要經過多少年,該樹的高度才能超過5米?(精確到個位)
(2)在第幾年內,該樹長高最快?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《鄭州市城市生活垃圾分類管理辦法》已經政府常務會議審議通過,自2019年12月1日起施行.垃圾分類是對垃圾收集處置傳統方式的改革,是對垃圾進行有效處置的一種科學管理方法.所謂垃圾其實都是資源,當你放錯了位置時它才是垃圾.某企業在市科研部門的支持下進行研究,把廚余垃圾加工處理為一種可銷售的產品.已知該企業每周的加工處理量最少為75噸,最多為100噸.周加工處理成本y(元)與周加工處理量x(噸)之間的函數關系可近似地表示為![]() ,且每加工處理一噸廚余垃圾得到的產品售價為16元.
,且每加工處理一噸廚余垃圾得到的產品售價為16元.
(Ⅰ)該企業每周加工處理量為多少噸時,才能使每噸產品的平均加工處理成本最低?
(Ⅱ)該企業每周能否獲利?如果獲利,求出利潤的最大值;如果不獲利,則需要市政府至少補貼多少元才能使該企業不虧損?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() :
:![]() ,圓
,圓![]() :
:![]() .以坐標原點
.以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求圓![]() ,
,![]() 的極坐標方程;
的極坐標方程;
(2)設![]() ,
,![]() 分別為
分別為![]() ,
,![]() 上的點,若
上的點,若![]() 為等邊三角形,求
為等邊三角形,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,下頂點為
,下頂點為![]() ,
,![]() 為橢圓的左、右焦點,過右焦點的直線與橢圓交于
為橢圓的左、右焦點,過右焦點的直線與橢圓交于![]() 兩點,且
兩點,且![]() 的周長為
的周長為![]() .
.
(I)求橢圓![]() 的方程;
的方程;
(II)經過點![]() 的直線與橢圓
的直線與橢圓![]() 交于不同的兩點
交于不同的兩點![]() (均異于點
(均異于點![]() ),試探求直線
),試探求直線![]() 與
與![]() 的斜率之和是否為定值,證明你的結論.
的斜率之和是否為定值,證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,長方體ABCD﹣A1B1C1D1中,AD=AA1=1,AB=m,點M是棱CD的中點.
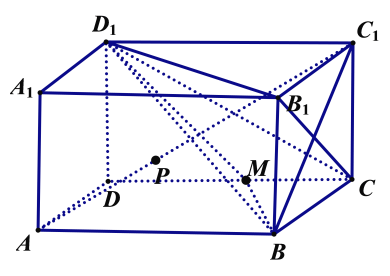
(1)求異面直線B1C與AC1所成的角的大小;
(2)是否存在實數m,使得直線AC1與平面BMD1垂直?說明理由;
(3)設P是線段AC1上的一點(不含端點),滿足![]() λ,求λ的值,使得三棱錐B1﹣CD1C1與三棱錐B1﹣CD1P的體積相等.
λ,求λ的值,使得三棱錐B1﹣CD1C1與三棱錐B1﹣CD1P的體積相等.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:![]() 經過點
經過點![]() ,其焦點為F,M為拋物線上除了原點外的任一點,過M的直線l與x軸、y軸分別交于A,B兩點.
,其焦點為F,M為拋物線上除了原點外的任一點,過M的直線l與x軸、y軸分別交于A,B兩點.
![]() Ⅰ
Ⅰ![]() 求拋物線C的方程以及焦點坐標;
求拋物線C的方程以及焦點坐標;
![]() Ⅱ
Ⅱ![]() 若
若![]() 與
與![]() 的面積相等,證明直線l與拋物線C相切.
的面積相等,證明直線l與拋物線C相切.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com