
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,下頂點為
,下頂點為![]() ,
,![]() 為橢圓的左、右焦點,過右焦點的直線與橢圓交于
為橢圓的左、右焦點,過右焦點的直線與橢圓交于![]() 兩點,且
兩點,且![]() 的周長為
的周長為![]() .
.
(I)求橢圓![]() 的方程;
的方程;
(II)經過點![]() 的直線與橢圓
的直線與橢圓![]() 交于不同的兩點
交于不同的兩點![]() (均異于點
(均異于點![]() ),試探求直線
),試探求直線![]() 與
與![]() 的斜率之和是否為定值,證明你的結論.
的斜率之和是否為定值,證明你的結論.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】“科技引領,布局未來”科技研發是企業發展的驅動力量。![]() 年,某企業連續
年,某企業連續![]() 年累計研發投入搭
年累計研發投入搭![]() 億元,我們將研發投入與經營投入的比值記為研發投入占營收比,這
億元,我們將研發投入與經營投入的比值記為研發投入占營收比,這![]() 年間的研發投入(單位:十億元)用右圖中的折現圖表示,根據折線圖和條形圖,下列結論錯誤的使( )
年間的研發投入(單位:十億元)用右圖中的折現圖表示,根據折線圖和條形圖,下列結論錯誤的使( )
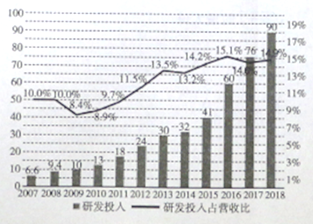
A. ![]() 年至
年至![]() 年研發投入占營收比增量相比
年研發投入占營收比增量相比![]() 年至
年至![]() 年增量大
年增量大
B. ![]() 年至
年至![]() 年研發投入增量相比
年研發投入增量相比![]() 年至
年至![]() 年增量小
年增量小
C. 該企業連續![]() 年研發投入逐年增加
年研發投入逐年增加
D. 該企業來連續![]() 年來研發投入占營收比逐年增加
年來研發投入占營收比逐年增加
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中,正確的個數是( )
(1)在頻率分布直方圖中,中位數左邊和右邊的直方圖的面積相等.
(2)如果一組數中每個數減去同一個非零常數,則這一組數的平均數改變,方差不改變.
(3)一個樣本的方差s2=![]() [(x
[(x![]() 一3)2+(X
一3)2+(X![]() —3)2+ +(X
—3)2+ +(X![]() 一3)2],則這組數據總和等于60.
一3)2],則這組數據總和等于60.
(4)數據![]() 的方差為
的方差為![]() ,則數據
,則數據![]() 的方差為
的方差為![]() .
.
A.4B.3C.2D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網絡營銷部門為了統計某市網友某日在某淘寶店的網購情況,隨機抽查了該市當天![]() 名網友的網購金額情況,得到如下統計表(如圖).
名網友的網購金額情況,得到如下統計表(如圖).
網購金額(單位:千元) | 頻數 | 頻率 |
| 3 | 0.05 |
|
|
|
| 9 | 0.15 |
| 15 | 0.25 |
| 18 | 0.30 |
|
|
|

若網購金額超過![]() 千元的顧客定義為“網購達人”,網購金額不超過
千元的顧客定義為“網購達人”,網購金額不超過![]() 千元的顧客定義為“非網購達人”,已知“非網購達人”與“網購達人”人數比恰好為
千元的顧客定義為“非網購達人”,已知“非網購達人”與“網購達人”人數比恰好為![]() .
.
(Ⅰ)試確定![]() 的值,并補全頻率分布直方圖(如圖);
的值,并補全頻率分布直方圖(如圖);
(Ⅱ)該營銷部門為了進一步了解這![]() 名網友的購物體驗,從“非網購達人”與“網購達人”中用分層抽樣的方法抽取
名網友的購物體驗,從“非網購達人”與“網購達人”中用分層抽樣的方法抽取![]() 人,若需從這
人,若需從這![]() 人中隨機選取
人中隨機選取![]() 人進行問卷調查.設
人進行問卷調查.設![]() 為選取的
為選取的![]() 人中“網購達人”的人數,求
人中“網購達人”的人數,求![]() 的分布列及其數學期望.
的分布列及其數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設直線![]() 與平面
與平面![]() 相交但不垂直,則下列說法中正確的是( )
相交但不垂直,則下列說法中正確的是( )
A.在平面![]() 內沒有直線與直線
內沒有直線與直線![]() 垂直;
垂直;
B.在平面![]() 內有且只有一條直線與直線
內有且只有一條直線與直線![]() 垂直;
垂直;
C.在平面![]() 內有無數條直線與直線
內有無數條直線與直線![]() 垂直;
垂直;
D.在平面![]() 內存在兩條相交直線與直線
內存在兩條相交直線與直線![]() 垂直.
垂直.
查看答案和解析>>
科目:高中數學 來源: 題型:
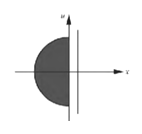
【題目】關于旋轉體的體積,有如下的古爾丁(guldin)定理:“平面上一區域D繞區域外一直線(區域D的每個點在直線的同側,含直線上)旋轉一周所得的旋轉體的體積,等于D的面積與D的幾何中心(也稱為重心)所經過的路程的乘積”.利用這一定理,可求得半圓盤 ,繞直線x
,繞直線x![]() 旋轉一周所形成的空間圖形的體積為_____.
旋轉一周所形成的空間圖形的體積為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,底面ABCD為矩形,PA⊥平面ABCD,E為PD的中點.

(1) 證明:PB∥平面AEC
(2) 設二面角D-AE-C為60°,AP=1,AD=![]() ,求三棱錐E-ACD的體積
,求三棱錐E-ACD的體積
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 中,邊
中,邊![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,![]() ,過
,過![]() 邊上一點
邊上一點![]() (異于端點)引邊
(異于端點)引邊![]() 的垂線
的垂線![]() ,垂足為
,垂足為![]() ,再由
,再由![]() 引邊
引邊![]() 的垂線
的垂線![]() ,垂足為
,垂足為![]() ,又由
,又由![]() 引邊
引邊![]() 的垂線
的垂線![]() ,垂足為
,垂足為![]() ,同樣的操作連續進行,得到點列
,同樣的操作連續進行,得到點列![]() 、
、![]() 、
、![]() ,設
,設![]() (
(![]() );
);
(1)求![]() ;
;
(2)結論“![]() ”是否正確?請說明理由;
”是否正確?請說明理由;
(3)若對于任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com