
【題目】在四棱錐P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC與BD的交點M恰好是AC中點,又PA=4,AB=4 ![]() ,∠CDA=120°,點N在線段PB上,且PN=2.
,∠CDA=120°,點N在線段PB上,且PN=2. 
(1)求證:BD⊥PC;
(2)求證:MN∥平面PDC;
(3)求二面角A﹣PC﹣B的余弦值.
【答案】
(1)證明:∵△ABC是正三角形,M是AC中點,
∴BM⊥AC,即BD⊥AC,
又∵PA⊥平面ABCD,∴PA⊥BD,
又PA∩AC=A,∴BD⊥平面PAC,
∴BD⊥PC.
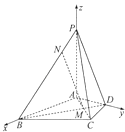
(2)證明:在正△ABC中,BM=6,
在△ACD中,∵M為AC中點,DM⊥AC,∴AD=CD,
∠ADC=120°,∴DM=2,
∴ ![]() =
= ![]() ,
,
在Rt△PAB中,PA=4,AB=4 ![]() ,PB=8.
,PB=8.
∴ ![]() =
= ![]() =
= ![]() ,∴MN∥PD,
,∴MN∥PD,
又MN平面PDC,PD平面平面PDC,
∴MN∥平面PDC.
(3)解:∵∠BAD=∠BAC+∠CAD=90°,
∴AB⊥AD,以A為坐標原點,分別以AB、AD、AP所在直線為x軸,y軸,z軸,建立空間直角坐標系,
∴B(4 ![]() ,0,0),C(2
,0,0),C(2 ![]() ,6,0),D(0,4,0),P(0,0,4),
,6,0),D(0,4,0),P(0,0,4),
![]() =(2
=(2 ![]() ,6,﹣4),
,6,﹣4), ![]() =(4
=(4 ![]() ,0,﹣4),
,0,﹣4),
由(2)知 ![]() =(4
=(4 ![]() ,﹣4,0)是平面PAC的法向量,
,﹣4,0)是平面PAC的法向量,
設平面PBC的一個法向量為 ![]() =(x,y,z),
=(x,y,z),
則  ,即
,即 ![]() ,取z=3,得
,取z=3,得 ![]() =(
=( ![]() ),
),
設二面角A﹣PC﹣B的平面角為θ,
則cosθ= ![]() =
= ![]() =
= ![]() ,
,
∴二面角A﹣PC﹣B的余弦值為 ![]() .
.
【解析】(1)導出BD⊥AC,PA⊥BD,從而BD⊥平面PAC,由此能證明BD⊥PC.(2)推導出DM⊥AC,AD=CD,DM=2, ![]() =
= ![]() ,從而MN∥PD,由此能證明MN∥平面PDC.(3)以A為坐標原點,分別以AB、AD、AP所在直線為x軸,y軸,z軸,建立空間直角坐標系,利用向量法能求出二面角A﹣PC﹣B的余弦值.
,從而MN∥PD,由此能證明MN∥平面PDC.(3)以A為坐標原點,分別以AB、AD、AP所在直線為x軸,y軸,z軸,建立空間直角坐標系,利用向量法能求出二面角A﹣PC﹣B的余弦值.


 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:高中數學 來源: 題型:
【題目】某中學高三年級從甲、乙兩個班級各選出7名學生參加數學競賽,他們取得的成績(滿分100分)的莖葉圖如圖,其中甲班學生成績的中位數是83,乙班學生成績的平均數是86,則x+y的值為( ) 
A.168
B.169
C.8
D.9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB⊥CD,AD∥BC,AD=3,BC=2AB=2,E,F分別在BC,AD上,EF∥AB.現將四邊形ABEF沿EF折起,使平面ABEF⊥平面EFDC.
(Ⅰ)若BE= ![]() ,在折疊后的線段AD上是否存在一點P,且
,在折疊后的線段AD上是否存在一點P,且 ![]() ,使得CP∥平面ABEF?若存在,求出λ的值,若不存在,說明理由;
,使得CP∥平面ABEF?若存在,求出λ的值,若不存在,說明理由;
(Ⅱ)求三棱錐A﹣CDF的體積的最大值,并求此時二面角E﹣AC﹣F的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】f(x)是定義在(0,+∞)上單調函數,且對x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,則方程f(x)﹣f′(x)=e的實數解所在的區間是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(1,e)
D.(e,3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線E:y2=2px(p>0)的準線與x軸交于點K,過點K作圓(x﹣5)2+y2=9的兩條切線,切點為M,N,|MN|=3 ![]()
(1)求拋物線E的方程;
(2)設A,B是拋物線E上分別位于x軸兩側的兩個動點,且 ![]() (其中O為坐標原點).
(其中O為坐標原點).
①求證:直線AB必過定點,并求出該定點Q的坐標;
②過點Q作AB的垂線與拋物線交于G,D兩點,求四邊形AGBD面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2 ![]() sin
sin ![]() cos
cos ![]() ﹣2sin2
﹣2sin2 ![]() (ω>0)的最小正周期為3π.
(ω>0)的最小正周期為3π.
(I)求函數f(x)的單調遞增區間;
(Ⅱ)在△ABC中,a,b,c分別為角A,B,C所對的邊,a<b<c, ![]() a=2csinA,并且f(
a=2csinA,并且f( ![]() A+
A+ ![]() )=
)= ![]() ,求cosB的值.
,求cosB的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在長方體ABCD﹣A1B1C1D1中,AA1=AD=a,E為CD上任意一點.
(I)求證:B1E⊥AD1;
(Ⅱ)若CD= ![]() a,是否存在這樣的E點,使得AD1與平面B1AE成45°的角?說明理由.
a,是否存在這樣的E點,使得AD1與平面B1AE成45°的角?說明理由.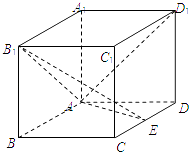
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com