
【題目】如圖,四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 為梯形,
為梯形,![]() ,
,![]() ,
,![]() ,且
,且![]() 與
與![]() 均為正三角形,
均為正三角形,![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 重心.
重心.

(1)求證:![]() 平面
平面![]() ;
;
(2)求三棱錐![]() 的體積.
的體積.
【答案】(Ⅰ)詳見解析(Ⅱ)![]()
【解析】
試題分析: (Ⅰ)連接![]() 與
與![]() 交于
交于![]() ,連接
,連接![]() .在梯形
.在梯形![]() 中,根據兩平行邊的比例,可得
中,根據兩平行邊的比例,可得![]() 的比值,在
的比值,在![]() 中,由重心的性質,可得
中,由重心的性質,可得![]() 間的比值,兩比值相等,則
間的比值,兩比值相等,則![]() ,再由線線平行去證明線面平行; (Ⅱ)根據所給條件可證
,再由線線平行去證明線面平行; (Ⅱ)根據所給條件可證![]() ,且求出
,且求出![]() 的長.由
的長.由![]() ,可將所求三棱錐
,可將所求三棱錐![]() 的體轉化為求三棱錐
的體轉化為求三棱錐![]() 體積,再轉化為三棱錐
體積,再轉化為三棱錐![]() 體積,又
體積,又![]() ,只需求
,只需求![]() 即可.
即可.
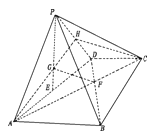
試題解析:(Ⅰ)方法一:連![]() 交
交![]() 于
于![]() ,連接
,連接![]() .
.
由梯形![]() ,
,![]() 且
且![]() ,知
,知![]()
又![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的重心,∴
的重心,∴![]()
在![]() 中,
中,![]() ,故
,故![]() //
//![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() //平面
//平面![]() .
.
方法二:過![]() 作
作![]() 交
交![]() 于
于![]() ,過
,過![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,
,
![]()
![]() 為
為![]() 的重心,
的重心,![]() ,
,![]() ,
,
又![]() 為梯形,
為梯形,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ∴
∴![]()
又由所作![]() ,
,![]() 得
得![]() //
//![]() ,
,![]() 為平行四邊形.
為平行四邊形.
![]() ,
,![]()
![]() 面
面![]()

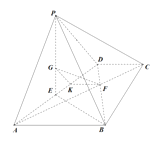
方法三:過![]() 作
作![]() //
//![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,
,
由![]() 為正三角形,
為正三角形, ![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 重心,
重心,
得![]() ,
,![]()
又由梯形![]() ,
,![]() ,且
,且![]() ,
,
知![]() ,即
,即![]()
∴在![]() 中,
中,![]() //
//![]() ,所以平面
,所以平面![]() //平面
//平面![]()
又![]() 平面
平面![]() ,∴
,∴![]() 面
面![]()
(Ⅱ) 方法一:由平面![]() 平面
平面![]() ,
,![]() 與
與![]() 均為正三角形,
均為正三角形,![]() 為
為![]() 的中點
的中點
∴![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,且
,且![]()
由(Ⅰ)知![]() //平面
//平面![]() ,∴
,∴![]()
又由梯形![]() ,
,![]() ,且
,且![]() ,知
,知![]()
又![]() 為正三角形,得
為正三角形,得![]() ,∴
,∴![]() ,
,
得![]()
∴三棱錐![]() 的體積為
的體積為![]() .
.
方法二: 由平面![]() 平面
平面![]() ,
,![]() 與
與![]() 均為正三角形,
均為正三角形,![]() 為
為![]() 的中點
的中點
∴![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,且
,且![]()
由![]() ,∴
,∴![]()
而又![]() 為正三角形,得
為正三角形,得![]() ,得
,得![]() .
.
∴![]() ,∴三棱錐
,∴三棱錐![]() 的體積為
的體積為![]() .
.


科目:高中數學 來源: 題型:
【題目】在四棱錐P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC與BD的交點M恰好是AC中點,又PA=4,AB=4 ![]() ,∠CDA=120°,點N在線段PB上,且PN=2.
,∠CDA=120°,點N在線段PB上,且PN=2. 
(1)求證:BD⊥PC;
(2)求證:MN∥平面PDC;
(3)求二面角A﹣PC﹣B的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,已知3acosA=ccosB+bcosC.
(1)求cosA,sinA的值;
(2)若cosB+cosC= ![]() ,求cosC+
,求cosC+ ![]() sinC的值.
sinC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某市民眾對某項公共政策的態度,在該市隨機抽取了![]() 名市民進行調查,做出了他們的月收入(單位:百元,范圍:
名市民進行調查,做出了他們的月收入(單位:百元,范圍:![]() )的頻率分布直方圖,同時得到他們月收入情況以及對該項政策贊成的人數統計表:
)的頻率分布直方圖,同時得到他們月收入情況以及對該項政策贊成的人數統計表:
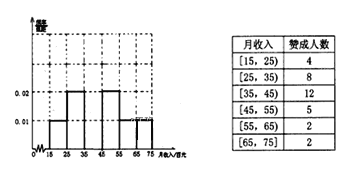
(1)求月收入在![]() 內的頻率,并補全這個頻率分布直方圖,并在圖中標出相應縱坐標;
內的頻率,并補全這個頻率分布直方圖,并在圖中標出相應縱坐標;
(2)根據頻率分布直方圖估計這![]() 人的平均月收入;
人的平均月收入;
(3)若從月收入(單位:百元)在![]() 的被調查者中隨機選取
的被調查者中隨機選取![]() 人,求
人,求![]() 人都不贊成的概率.
人都不贊成的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a∈R,函數f(x)=log2( ![]() +a).
+a).
(1)當a=5時,解不等式f(x)>0;
(2)若關于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一個元素,求a的取值范圍.
(3)設a>0,若對任意t∈[ ![]() ,1],函數f(x)在區間[t,t+1]上的最大值與最小值的差不超過1,求a的取值范圍.
,1],函數f(x)在區間[t,t+1]上的最大值與最小值的差不超過1,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,已知C= ![]() ,向量
,向量 ![]() =(sinA,1),
=(sinA,1), ![]() =(1,cosB),且
=(1,cosB),且 ![]() .
.
(1)求A的值;
(2)若點D在邊BC上,且3 ![]() =
= ![]() ,
, ![]() =
= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設p:實數x滿足x2﹣4ax+3a2<0,其中a>0; q:實數x滿足 ![]() <0.
<0.
(1)若a=1,且p∨q為真,求實數x的取值范圍;
(2)若p是q的必要不充分條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學著作《九章算術》有如下問題:“今有人持金出五關,前關二而稅一,次關三而稅一,次關四而稅一,次關五而稅一,次關六而稅一,并五關所稅,適重一斤,問本持金幾何”其意思為“今有人持金出五關,第1關收稅金 ![]() ,第2關收稅金為剩余金的
,第2關收稅金為剩余金的 ![]() ,第3關收稅金為剩余金的
,第3關收稅金為剩余金的 ![]() ,第4關收稅金為剩余金的
,第4關收稅金為剩余金的 ![]() ,第5關收稅金為剩余金的
,第5關收稅金為剩余金的 ![]() ,5關所收稅金之和,恰好重1斤,問原來持金多少?”若將題中“5關所收稅金之和,恰好重1斤,問原來持金多少?”改成假設這個原來持金為x,按此規律通過第8關,則第8關需收稅金為x.
,5關所收稅金之和,恰好重1斤,問原來持金多少?”若將題中“5關所收稅金之和,恰好重1斤,問原來持金多少?”改成假設這個原來持金為x,按此規律通過第8關,則第8關需收稅金為x.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com