
分析 (1)利用二項式定理系數的性質,求出xn的系數,即可得到結論.
(2)利用已知關系式,求出等式兩邊的常數項系數,即可得到結果.
解答 解:(1)${C}_{m+n}^{k}$=${{C}_{m}^{0}C}_{n}^{k}$+${{C}_{m}^{1}C}_{n}^{k-1}$+…+${{C}_{m}^{k}C}_{n}^{0}$=${C}_{m+m}^{k}$.
證明:(2)考察等式(2+x+$\frac{1}{x}$)n=$\frac{(x+1)^{2n}}{{x}^{n}}$,
等式右邊的常數項為:$\frac{{C}_{2n}^{n}{x}^{n}}{{x}^{n}}{=C}_{2n}^{n}$,
∵$(2+x+\frac{1}{x})^{n}={\sum_{i=0}^{n}C}_{n}^{r}$•2n-r(x+$\frac{1}{x}$)r=${\sum_{i=0}^{n}C}_{n}^{r}$•2n-r(${\sum_{i=0}^{r}C}_{i}^{k}$$•{x}^{i-k}(\frac{1}{x})^{k})$,
當且僅當i=2k時,xr-k($\frac{1}{x}$)k為常數,
等式左邊的常數項為:$\sum_{k=0}^{[{\frac{n}{2}}]}{C_n^{2k}}•{2^{n-2k}}•C_{2k}$k,
∴$\sum_{k=0}^{[{\frac{n}{2}}]}{C_n^{2k}}•{2^{n-2k}}•C_{2k}$k=Cnn成立.
點評 本題主要考查二項式定理等基礎知識,考查推理論證能力,屬于中檔題.


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若m∥n,m⊥α,則n⊥α | B. | 若m∥α,m∥β,則α∥β | C. | 若m∥α,n∥α,則m∥n | D. | 若m∥α,α⊥β,則m⊥β |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{2\sqrt{2}}}{81}π$ | B. | $\frac{{4\sqrt{5}}}{81}π$ | C. | $\frac{8}{81}π$ | D. | $\frac{10}{81}π$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
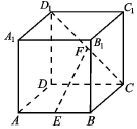 正方體ABCD-A1B1C1D1中,E為AB中點,F為CD1中點.
正方體ABCD-A1B1C1D1中,E為AB中點,F為CD1中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com