
分析 (1)根據函數周期的定義進行證明即可.
(2)由f(x)最小正周期為4,知當x∈[2,4]時,有f(-x)=f(-x+4),根據奇函數的性質推知f(x)=-f(-x),由此得到f(x)的解析式;
(3)利用定積分的計算公式解答.
解答 (1)證明:∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=-[-f(x)]=f(x),
即函數f(x)是周期為4的周期函數.
(2)解:x∈[2,4],則-x∈[-2,-4],-x+4∈[0,2],
∵函數f(x)是周期為4的周期函數,
∴f(-x)=f(-x+4)=2(4-x)-(4-x)2
又因為f(x)是奇函數,所以f(x)=-f(-x)=x2-6x+8.
(3)解:${∫}_{0}^{4}$f(x)dx
=${∫}_{0}^{2}$(2x-x2)dx+${∫}_{2}^{4}$(x2-6x+8)dx
=($-\frac{1}{3}$x3+x2)|$\left.\begin{array}{l}{2}\\{0}\end{array}\right.$+($\frac{1}{3}$x3-3x2+8x)|$\left.\begin{array}{l}{4}\\{2}\end{array}\right.$
=$-\frac{1}{3}$×23+22+$\frac{1}{3}$×43-3×42+8×4-$\frac{1}{3}$×23+3×22-8×2
=0.
點評 本題考查函數的周期性質的應用,是基礎題,解題時要認真審題,仔細解答,注意合理地進行等價轉化.


 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
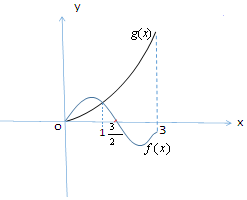 已知函數y=f(x)是偶函數,y=g(x)是奇函數,它們的定義域是[-3,3],它們在x∈[0,3]上的圖象如圖所示,則不等式f(x)•g(x)≥0的解集是[-3,-$\frac{3}{2}$]∪[0,$\frac{3}{2}$].
已知函數y=f(x)是偶函數,y=g(x)是奇函數,它們的定義域是[-3,3],它們在x∈[0,3]上的圖象如圖所示,則不等式f(x)•g(x)≥0的解集是[-3,-$\frac{3}{2}$]∪[0,$\frac{3}{2}$].查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 函數y=f(x)•g(x)的最小正周期為2π | |
| B. | 函數y=f(x)•g(x)的最大值為1 | |
| C. | $x=\frac{π}{2}$是函數y=f(x)•g(x)的圖象的一條對稱軸 | |
| D. | 函數y=f(x)•g(x)在區間$[-\frac{π}{4},\frac{π}{4}]$是單調增函數 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com