
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的零點;
的零點;
(2)設(shè)函數(shù)![]() 的圖象與函數(shù)
的圖象與函數(shù)![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點,求證:
兩點,求證:![]() ;
;
(3)若![]() ,且不等式
,且不等式![]() 對一切正實數(shù)x恒成立,求k的取值范圍.
對一切正實數(shù)x恒成立,求k的取值范圍.
【答案】(1)x=1 (2)證明見解析 (3) ![]()
【解析】
(1)令![]() ,根據(jù)導(dǎo)函數(shù)確定函數(shù)的單調(diào)區(qū)間,求出極小值,進而求解;
,根據(jù)導(dǎo)函數(shù)確定函數(shù)的單調(diào)區(qū)間,求出極小值,進而求解;
(2)轉(zhuǎn)化思想,要證![]()
![]() ,即證
,即證![]()
![]()
![]() ,即證
,即證![]() ,構(gòu)造函數(shù)進而求證;
,構(gòu)造函數(shù)進而求證;
(3)不等式![]() 對一切正實數(shù)
對一切正實數(shù)![]() 恒成立,
恒成立,![]() ,設(shè)
,設(shè)![]() ,分類討論進而求解.
,分類討論進而求解.
解:(1)令![]() ,所以
,所以![]() ,
,
當(dāng)![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
當(dāng)![]() 時,
時,![]() ,
,![]() 在
在![]() 單調(diào)遞減;
單調(diào)遞減;
所以![]() ,所以
,所以![]() 的零點為
的零點為![]() .
.
(2)由題意![]()
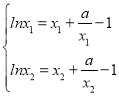 ,
, ![]() ,
,
要證![]()
![]() ,即證
,即證![]() ,即證
,即證![]() ,
,
令![]() ,則
,則![]() ,由(1)知
,由(1)知![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() 時等號成立,所以
時等號成立,所以![]() ,
,
即![]() ,所以原不等式成立.
,所以原不等式成立.
(3)不等式![]() 對一切正實數(shù)
對一切正實數(shù)![]() 恒成立,
恒成立,
![]() ,
,
設(shè)![]() ,
,![]() ,
,
記![]() ,△
,△![]() ,
,
①當(dāng)△![]() 時,即
時,即![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 單調(diào)遞增.
單調(diào)遞增.
于是當(dāng)![]() 時,
時,![]() ,又
,又![]() ,故
,故![]() ,
,
當(dāng)![]() 時,
時,![]() ,又
,又![]() ,故
,故![]() ,
,
又當(dāng)![]() 時,
時,![]() ,
,
因此,當(dāng)![]() 時,
時,![]() ,
,
②當(dāng)△![]() ,即
,即![]() 時,設(shè)
時,設(shè)![]() 的兩個不等實根分別為
的兩個不等實根分別為![]() ,
,![]() ,
,
又![]() ,于是
,于是![]() ,
,
故當(dāng)![]() 時,
時,![]() ,從而
,從而![]() 在
在![]() 單調(diào)遞減;
單調(diào)遞減;
當(dāng)![]() 時,
時,![]() ,此時
,此時![]() ,于是
,于是![]() ,
,
即![]() 舍去,
舍去,
綜上,![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)集合![]() ,設(shè)集合
,設(shè)集合![]() 是集合
是集合![]() 的非空子集,
的非空子集,![]() 中的最大元素和最小元素之差稱為集合
中的最大元素和最小元素之差稱為集合![]() 的直徑. 那么集合
的直徑. 那么集合![]() 所有直徑為
所有直徑為![]() 的子集的元素個數(shù)之和為( )
的子集的元素個數(shù)之和為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 是單調(diào)遞增函數(shù),求實數(shù)a的取值范圍;
是單調(diào)遞增函數(shù),求實數(shù)a的取值范圍;
(2)若![]() 恒成立,求實數(shù)a的取值范圍.
恒成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】惰性氣體分子為單原子分子,在自由原子情形下,其電子電荷分布是球?qū)ΨQ的.負電荷中心與原子核重合,但如兩個原子接近,則彼此能因靜電作用產(chǎn)生極化(正負電荷中心不重合),從而導(dǎo)致有相互作用力,這稱為范德瓦爾斯相互作用.今有兩個相同的惰性氣體原子,它們的原子核固定,原子核正電荷的電荷量為![]() ,這兩個相距為
,這兩個相距為![]() 的惰性氣體原子組成體系的能量中有靜電相互作用能
的惰性氣體原子組成體系的能量中有靜電相互作用能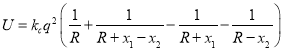 ,其中
,其中![]() 為靜電常量,
為靜電常量,![]() ,
,![]() 分別表示兩個原子負電中心相對各自原子核的位移,且
分別表示兩個原子負電中心相對各自原子核的位移,且![]() 和
和![]() 都遠小于
都遠小于![]() ,當(dāng)
,當(dāng)![]() 遠小于1時,
遠小于1時,![]() ,則
,則![]() 的近似值為( )
的近似值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)求函數(shù)![]() 的零點和極值;
的零點和極值;
(3)若對任意![]() ,都有
,都有![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若![]() ,不等式
,不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點F1為橢圓![]() 的左焦點,
的左焦點,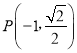 在橢圓上,PF1⊥x軸.
在橢圓上,PF1⊥x軸.
(1)求橢圓的方程:
(2)已知直線l與橢圓交于A,B兩點,且坐標(biāo)原點O到直線l的距離為![]() 的大小是否為定值?若是,求出該定值:若不是,請說明理由.
的大小是否為定值?若是,求出該定值:若不是,請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com