考點:函數恒成立問題,函數的定義域及其求法,函數奇偶性的判斷
專題:函數的性質及應用,不等式的解法及應用
分析:(1)直接由對數式的真數大于0聯立不等式組得答案;
(2)直接運用奇函數的概念加以判斷證明;
(3)把f(x)<log
2(ax)在x∈[
,1]上恒成立轉化為二次函數恒成立問題,然后結合二次函數的對稱軸及單調性列式求解a的范圍.
解答:
解:(1)由f(x)=log
2(2-x)-log
2(x+2).
要使原函數有意義,則
,解得-2<x<2.
∴函數f(x)的定義域為(-2,2);
(2)f(x)為定義域內的奇函數.
事實上,∵f(-x)=log
2(2+x)-log
2(-x+2)=-f(x),
∴f(x)為定義域內的奇函數;
(3)f(x)<log
2(ax)在x∈[
,1]上恒成立,
即log
2(2-x)-log
2(x+2)<log
2(ax)在x∈[
,1]上恒成立,
也就是h(x)=ax
2+(2a+1)x-2>0在x∈[
,1]上恒成立,
又∵a>0,
則有h(
)=
a->0,解得:a
>.
點評:本題考查了函數定義域的求法,考查了函數奇偶性的判斷方法,訓練了利用二次函數求解恒成立問題,體現了數學轉化思想方法,是中檔題.



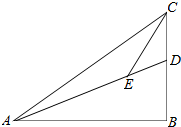 如圖,△ABC中,∠ABC=90°,點D在BC邊上,點E在AD上.
如圖,△ABC中,∠ABC=90°,點D在BC邊上,點E在AD上.