
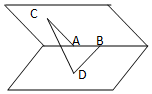
 如圖在一個60°的二面角的棱上有兩個點A、B,線段AC、BD分別在這個二面角的兩個面內,并且都垂直于棱AB,且AB=AC=1,BD=2,則CD的長為( )
如圖在一個60°的二面角的棱上有兩個點A、B,線段AC、BD分別在這個二面角的兩個面內,并且都垂直于棱AB,且AB=AC=1,BD=2,則CD的長為( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | 1 |
分析 由$\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$,兩邊平方后展開整理,即可求得${\overrightarrow{CD}}^{2}$,則CD的長可求.
解答 解:∵$\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$,
∴${\overrightarrow{CD}}^{2}={\overrightarrow{CA}}^{2}+{\overrightarrow{AB}}^{2}+{\overrightarrow{BD}}^{2}$+2$\overrightarrow{CA}•\overrightarrow{AB}$+2$\overrightarrow{CA}•\overrightarrow{BD}$+2$\overrightarrow{AB}•\overrightarrow{BD}$,
∵$\overrightarrow{CA}$⊥$\overrightarrow{AB}$,$\overrightarrow{BD}$⊥$\overrightarrow{AB}$,
∴$\overrightarrow{CA}•\overrightarrow{AB}=0$,$\overrightarrow{BD}•\overrightarrow{AB}=0$,
$\overrightarrow{CA}•\overrightarrow{BD}=|\overrightarrow{CA}||\overrightarrow{BD}|$cos120°=-$\frac{1}{2}$×1×2=-1.
∴${\overrightarrow{CD}}^{2}=1+1+4$-2×1=4,
∴|$\overrightarrow{CD}$|=2,
故選:A.
點評 本題考查了向量的多邊形法則、數量積的運算性質、向量垂直與數量積的關系,考查了空間想象能力,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
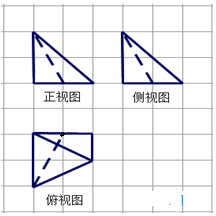 如圖,網格紙上小正方形的邊長為1,粗實線和虛線畫出的是某空間幾何體的三視圖,則該幾何體的體積為( )
如圖,網格紙上小正方形的邊長為1,粗實線和虛線畫出的是某空間幾何體的三視圖,則該幾何體的體積為( )| A. | 2 | B. | $\frac{2}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2n-1-2 | B. | 2n-2 | C. | 2n-1-2n | D. | -2n-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=|sinx| | B. | $y=cos({2x+\frac{π}{2}})$ | C. | y=sin2x+cos2x | D. | y=sinx-cosx |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com