
【題目】如圖,已知四棱錐![]() ,底面
,底面![]() 為矩形, 且側面
為矩形, 且側面![]() 平面
平面![]() ,側面
,側面![]() 平面
平面![]() ,
,![]() 為正三角形,
為正三角形,![]()

(1)求證:![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)見解析;(2)![]()
【解析】
![]() 因為
因為![]() ,所以
,所以![]() 平面
平面![]() ,由線面平行的性質定理推出結果
,由線面平行的性質定理推出結果
![]() 解法一:過
解法一:過![]() 作
作![]() 交
交![]() 于
于![]() ,結合
,結合![]() 可得
可得![]() 平面
平面![]() ,過
,過![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,所以
,所以![]() 即為直線
即為直線![]() 與平面
與平面![]() 所成角,然后解三角形;
所成角,然后解三角形;
解法二:以![]() 的中點為原點,建立空間坐標系
的中點為原點,建立空間坐標系![]() ,設
,設![]() ,設
,設![]() 與面
與面![]() 所成的角為
所成的角為![]() ,計算平面
,計算平面![]() 的一個法向量為
的一個法向量為![]() ,計算平面
,計算平面![]() 的一個法向量為
的一個法向量為![]() ,解得
,解得![]() ,代入求出結果
,代入求出結果
(1)因為![]() ,所以
,所以![]() 平面
平面![]() ;
;
又因為![]() 平面
平面![]() 且平面
且平面![]() 平面
平面![]() ,由線面平行的性質定理知
,由線面平行的性質定理知![]() .
.
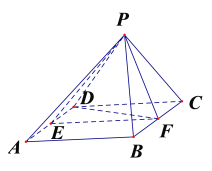
(2)過![]() 作
作![]() 交
交![]() 于
于![]() ,所以
,所以![]() .因為側面
.因為側面![]() 平面
平面![]() ,側面
,側面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,過
,過![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,所以
,所以![]() 即為直線
即為直線![]() 與平面
與平面![]() 所成角.
所成角.
又因為![]() ,所以
,所以![]() ,于是在
,于是在![]() 中,
中,![]() .
.
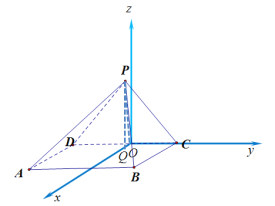
解法二:以![]() 的中點為原點,建立空間坐標系
的中點為原點,建立空間坐標系![]() ,設
,設![]() ,則
,則![]() ,
,![]() ,設
,設![]() 與面
與面![]() 所成的角為
所成的角為![]() ,由題意
,由題意![]() 點在面
點在面![]() 的射影
的射影![]() 必在
必在![]() 軸上,且由
軸上,且由![]() 是邊長為2的正三角形得
是邊長為2的正三角形得![]() ,所以
,所以
![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則
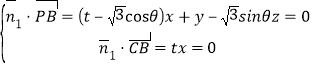 ,解得
,解得![]() ,
,
因為![]()
![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則
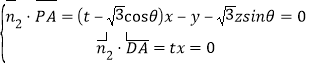 ,解得
,解得![]() ,
,
![]() ,
,
所以![]() ,
,![]() ,設直線
,設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,于是
,于是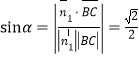 .
.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,四棱錐B-AEDC中,平面AEDC⊥平面ABC,F為BC的中點,P為BD的中點,且AE//DC,∠ACD=∠BAC=90°,DC=AC=AB=2AE
(1)證明:EP⊥平面BCD;
(2)若DC=2,求三棱錐E-BDF的體積.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】進入冬天,大氣流動性變差,容易形成霧握天氣,從而影響空氣質量.某城市環保部門試圖探究車流量與空氣質量的相關性,以確定是否對車輛實施限行.為此,環保部門采集到該城市過去一周內某時段車流量與空氣質量指數的數據如下表:
時間 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
車流量(x萬輛) | 10 | 9 | 9.5 | 10.5 | 11 | 8 | 8.5 |
空氣質量指數y | 78 | 76 | 77 | 79 | 80 | 73 | 75 |
(1)根據表中周一到周五的數據,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2,則認為得到的線性回歸方程是可靠的.請根據周六和周日數據,判定所得的線性回歸方程是否可靠?
附:回歸方程![]() 中斜率和截距最小二乘估計公式分別為:
中斜率和截距最小二乘估計公式分別為:
 其中:
其中:![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,曲線![]() ,
,![]() ,C與l有且僅有一個公共點.
,C與l有且僅有一個公共點.
(Ⅰ)求a;
(Ⅱ)O為極點,A,B為C上的兩點,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為常數,函數
為常數,函數![]() ,給出以下結論:
,給出以下結論:
(1)若![]() ,則
,則![]() 存在唯一零點
存在唯一零點
(2)若![]() ,則
,則![]()
(3)若![]() 有兩個極值點
有兩個極值點![]() ,則
,則![]()
其中正確結論的個數是( )
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據以往的經驗,某建筑工程施工期間的降水量![]() (單位:
(單位:![]() )對工期的影響如下表:
)對工期的影響如下表:
降水量 |
|
|
|
|
工期延誤天數 | 0 | 1 | 3 | 6 |
根據某氣象站的資料,某調查小組抄錄了該工程施工地某月前![]() 天的降水量的數據,繪制得到降水量的折線圖,如下圖所示.
天的降水量的數據,繪制得到降水量的折線圖,如下圖所示.

(1)根據降水量的折線圖,分別求該工程施工延誤天數![]() 的頻率;
的頻率;
(2)以(1)中的頻率作為概率,求工期延誤天數![]() 的分布列及數學期望與方差.
的分布列及數學期望與方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)對任意x,y∈R,總有f(x)+f(y)=f(x+y),且當x>0時,f(x)<0,f(1)=-![]() .
.
(1)求證:f(x)是R上的單調減函數.
(2)求f(x)在[-3,3]上的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com