
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過定點
,過定點![]() 的直線l與橢圓E相交于A,B兩點,C為橢圓的左頂點,當直線l過點
的直線l與橢圓E相交于A,B兩點,C為橢圓的左頂點,當直線l過點![]() 時,
時,![]() (O為坐標原點)的面積為
(O為坐標原點)的面積為![]() .
.
(1)求橢圓E的方程;
(2)求證:當直線l不過C點時,![]() 為定值.
為定值.
科目:高中數學 來源: 題型:
【題目】隨著現代電子技術的迅猛發展,關于元件和系統可靠性的研究已發展成為一門新的學科——可靠性理論.在可靠性理論中,一個元件正常工作的概率稱為該元件的可靠性.元件組成系統,系統正常工作的概率稱為該系統的可靠性.現有![]() (
(![]() ,
,![]() )種電子元件,每種2個,每個元件的可靠性均為
)種電子元件,每種2個,每個元件的可靠性均為![]() (
(![]() ).當某元件不能正常工作時,該元件在電路中將形成斷路.現要用這
).當某元件不能正常工作時,該元件在電路中將形成斷路.現要用這![]() 個元件組成一個電路系統,有如下兩種連接方案可供選擇,當且僅當從A到B的電路為通路狀態時,系統正常工作.
個元件組成一個電路系統,有如下兩種連接方案可供選擇,當且僅當從A到B的電路為通路狀態時,系統正常工作.
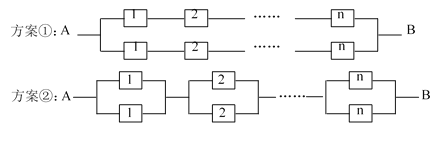
(1)(i)分別寫出按方案①和方案②建立的電路系統的可靠性![]() 、
、![]() (用
(用![]() 和
和![]() 表示);
表示);
(ii)比較![]() 與
與![]() 的大小,說明哪種連接方案更穩定可靠;
的大小,說明哪種連接方案更穩定可靠;
(2)設![]() ,
,![]() ,已知按方案②建立的電路系統可以正常工作,記此時系統中損壞的元件個數為
,已知按方案②建立的電路系統可以正常工作,記此時系統中損壞的元件個數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐![]() 中,底面
中,底面![]() 是邊長為4的正方形,
是邊長為4的正方形,![]() 為正三角形,
為正三角形,![]() 是
是![]() 的中點,過
的中點,過![]() 的平面
的平面![]() 平行于平面
平行于平面![]() ,且平面
,且平面![]() 與平面
與平面![]() 的交線為
的交線為![]() ,與平面
,與平面![]() 的交線為
的交線為![]() .
.
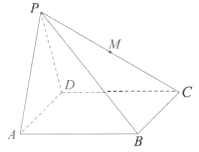
(1)在圖中作出四邊形![]() (不必說出作法和理由);
(不必說出作法和理由);
(2)若![]() ,求平面
,求平面![]() 與平面
與平面![]() 形成的銳二面角的余弦值.
形成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 為矩形,
為矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.
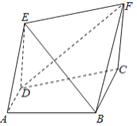
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,若存在,求出線段
,若存在,求出線段![]() 的長,若不存在,請說明理由.
的長,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】目前,我國老年人口比例不斷上升,造成日趨嚴峻的人口老齡化問題.2019年10月12日,北京市老齡辦、市老齡協會聯合北京師范大學中國公益研究院發布《北京市老齡事業發展報告(2018)》,相關數據有如下圖表.規定年齡在15歲至59歲為“勞動年齡”,具備勞動力,60歲及以上年齡為“老年人”,據統計,2018年底北京市每2.4名勞動力撫養1名老年人.
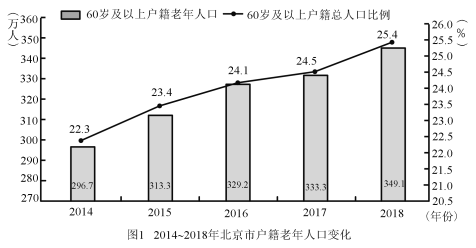
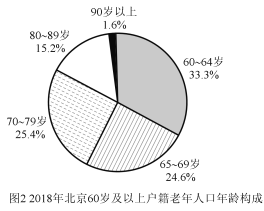
(Ⅰ)請根據上述圖表計算北京市2018年戶籍總人口數和北京市2018年的勞動力數;(保留兩位小數)
(Ⅱ)從2014年起,北京市老齡人口與年份呈線性關系,比照2018年戶籍老年人人口年齡構成,預計到2020年年底,北京市90以上老人達到多少人?(精確到1人)
(附:對于一組數據![]() 其回歸直線
其回歸直線![]() 的斜率和截距的最小二乘法估計分別為:
的斜率和截距的最小二乘法估計分別為: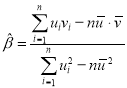 ,
,![]() .
.![]() ,
,![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com