
【題目】目前,我國老年人口比例不斷上升,造成日趨嚴峻的人口老齡化問題.2019年10月12日,北京市老齡辦、市老齡協會聯合北京師范大學中國公益研究院發布《北京市老齡事業發展報告(2018)》,相關數據有如下圖表.規定年齡在15歲至59歲為“勞動年齡”,具備勞動力,60歲及以上年齡為“老年人”,據統計,2018年底北京市每2.4名勞動力撫養1名老年人.
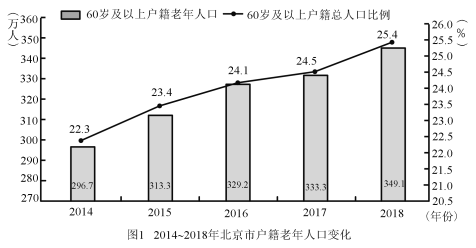
(Ⅰ)請根據上述圖表計算北京市2018年戶籍總人口數和北京市2018年的勞動力數;(保留兩位小數)
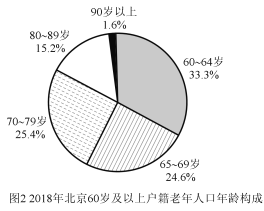
(Ⅱ)從2014年起,北京市老齡人口與年份呈線性關系,比照2018年戶籍老年人人口年齡構成,預計到2020年年底,北京市90以上老人達到多少人?(精確到1人)
(附:對于一組數據![]() 其回歸直線
其回歸直線![]() 的斜率和截距的最小二乘法估計分別為:
的斜率和截距的最小二乘法估計分別為: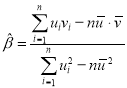 ,
,![]() .
.![]() ,
,![]() )
)
【答案】(Ⅰ)1374.41萬人837.84萬人(Ⅱ)59878人.
【解析】
(Ⅰ)由圖表數據及題意計算可得;
(Ⅱ)設2014年是第1年,第x年老年人口為y萬人,可得如下表格;依題意設![]() ,根據所給數據求出
,根據所給數據求出![]() ,
,![]() ,求出
,求出![]() 、
、![]() ,即可得得到回歸直線方程,再將
,即可得得到回歸直線方程,再將![]() 代入計算可得;
代入計算可得;
解:(Ⅰ)2018年北京市老年人349.1萬人,占戶籍總人口的25.4%,所以北京市2018年戶籍總人口![]() 萬人;
萬人;
2018年北京市“老年人”有349.1萬人,每2.4名勞動力撫養1名老年人,故北京市2018年的勞動力數為![]() 萬
萬
(Ⅱ)設2014年是第1年,第x年老年人口為y萬人,則
| 1 | 2 | 3 | 4 | 5 |
| 296.7 | 313.3 | 329.2 | 333.3 | 349.1 |
由于從2014年起,北京市老齡人口與年份呈線性關系,設![]()
則![]() ,
,![]() .
.
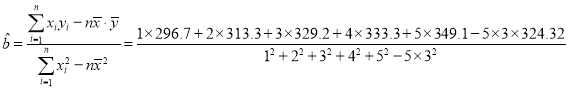
![]()
得![]()
∴![]()
當![]() 時,
時,![]()
∴北京市2020年年底的老年人人數約為374.24萬人,
90以上老人占1.6%,![]() 萬人≈59878人
萬人≈59878人
答:預計到2020年年底,北京市90以上老人約為59878人.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過定點
,過定點![]() 的直線l與橢圓E相交于A,B兩點,C為橢圓的左頂點,當直線l過點
的直線l與橢圓E相交于A,B兩點,C為橢圓的左頂點,當直線l過點![]() 時,
時,![]() (O為坐標原點)的面積為
(O為坐標原點)的面積為![]() .
.
(1)求橢圓E的方程;
(2)求證:當直線l不過C點時,![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在“挑戰不可能”的電視節目上,甲、乙、丙三個人組成的解密團隊參加一項解密挑戰活動,規則是由密碼專家給出題目,然后由![]() 個人依次出場解密,每人限定時間是
個人依次出場解密,每人限定時間是![]() 分鐘內,否則派下一個人.
分鐘內,否則派下一個人.![]() 個人中只要有一人解密正確,則認為該團隊挑戰成功,否則挑戰失敗.根據甲以往解密測試情況,抽取了甲
個人中只要有一人解密正確,則認為該團隊挑戰成功,否則挑戰失敗.根據甲以往解密測試情況,抽取了甲![]() 次的測試記錄,繪制了如下的頻率分布直方圖.
次的測試記錄,繪制了如下的頻率分布直方圖.
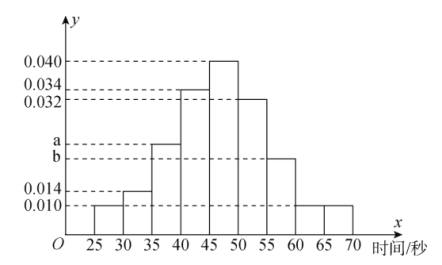
(1)若甲解密成功所需時間的中位數為![]() ,求
,求![]() 、
、![]() 的值,并求出甲在
的值,并求出甲在![]() 分鐘內解密成功的頻率;
分鐘內解密成功的頻率;
(2)在“挑戰不可能”節目上由于來自各方及自身的心理壓力,甲,乙,丙解密成功的概率分別為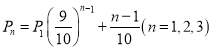 ,其中
,其中![]() 表示第
表示第![]() 個出場選手解密成功的概率,并且
個出場選手解密成功的概率,并且![]() 定義為甲抽樣中解密成功的頻率代替,各人是否解密成功相互獨立.
定義為甲抽樣中解密成功的頻率代替,各人是否解密成功相互獨立.
①求該團隊挑戰成功的概率;
②該團隊以![]() 從小到大的順序按排甲、乙、丙三個人上場解密,求團隊挑戰成功所需派出的人員數目
從小到大的順序按排甲、乙、丙三個人上場解密,求團隊挑戰成功所需派出的人員數目![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某病毒研究所為了研究溫度對某種病毒的影響,在溫度t(℃)逐漸升高時,連續測20次病毒的活性指標值y,實驗數據處理后得到下面的散點圖,將第1~14組數據定為A組,第15~20組數據定為B組.
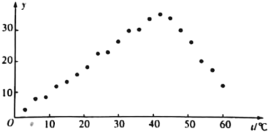
(Ⅰ)某研究員準備直接根據全部20組數據用線性回歸模型擬合y與t的關系,你認為是否合理?請從統計學的角度簡要說明理由.
(Ⅱ)若根據A組數據得到回歸模型![]() ,根據B組數據得到回歸模型
,根據B組數據得到回歸模型![]() ,以活性指標值大于5為標準,估計這種病毒適宜生存的溫度范圍(結果精確到0.1).
,以活性指標值大于5為標準,估計這種病毒適宜生存的溫度范圍(結果精確到0.1).
(Ⅲ)根據實驗數據計算可得:A組中活性指標值的平均數![]() ,方差
,方差![]()
![]() ;B組中活性指標值的平均數
;B組中活性指標值的平均數![]() ,方差
,方差![]() .請根據以上數據計算全部20組活性指標值的平均數
.請根據以上數據計算全部20組活性指標值的平均數![]() 和方差
和方差![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,四邊形ABCD為矩形,BC=2AB,E為AD的中點,將![]() ABE、
ABE、![]() DCE分別沿BE、CE折起得圖2,使得平面
DCE分別沿BE、CE折起得圖2,使得平面![]() 平面BCE,平面
平面BCE,平面![]() 平面BCE.
平面BCE.
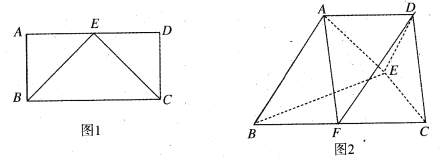
(1)求證:平面![]() 平面DCE;
平面DCE;
(2)若F為線段BC的中點,求直線FA與平面ADE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 與拋物線
與拋物線![]() 交于M,拋物線C的焦點為F,且
交于M,拋物線C的焦點為F,且![]() .
.
(Ⅰ)求拋物線C的方程;
(Ⅱ)設點Q是拋物線C上的動點,點D,E在y軸上,圓![]() 內切于三角形
內切于三角形![]() ,求三角形
,求三角形![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某市3月1日至14日的空氣質量指數趨勢圖.空氣質量指數小于100表示空氣質量優良,空氣質量指數大于200表示空氣重度污染.某人隨機選擇3月1日至3月13日中的某一天到達該市,并停留2天.
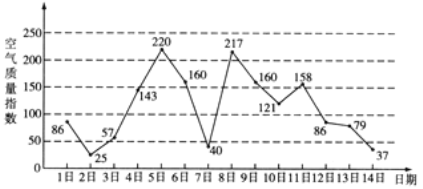
(1)求此人到達當日空氣重度污染的概率;
(2)求此人在該市停留期間只有1天空氣重度污染的概率;
(3)由圖判斷從哪天開始連續三天的空氣質量指數方差最大?(結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 上的點到
上的點到![]() 的距離比它到直線
的距離比它到直線![]() 的距離少3.
的距離少3.
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,交圓
兩點,交圓![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() ,
,![]() 在
在![]() 軸上方,過點
軸上方,過點![]() ,
,![]() 分別作曲線
分別作曲線![]() 的切線
的切線![]() ,
,![]() ,
,![]() ,求
,求![]() 與
與![]() 的面積的積的取值范圍.
的面積的積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
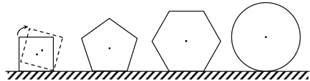
【題目】現有邊長均為1的正方形正五邊形正六邊形及半徑為1的圓各一個,在水平桌面上無滑動滾動一周,它們的中心的運動軌跡長分別為![]() ,
,![]() ,
,![]() ,
,![]() ,則( )
,則( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com