Question

12．已知O是△ABC外接圓的圓心，已知△ABC外接圓半徑為2，若$4\overrightarrow{OA}+5\overrightarrow{OB}+6\overrightarrow{OC}=\vec 0$，則邊長AB=3．

Answer 1

分析 由$4\overrightarrow{OA}+5\overrightarrow{OB}+6\overrightarrow{OC}=\vec 0$，得16R²+25R²+40R²cos∠AOB=36R²，即8cos∠AOB=-1，
由2∠ACB=∠AOB，得cosC=$\frac{\sqrt{7}}{4}$⇒sin∠ACB=$\frac{3}{4}$
由$\frac{AB}{sin∠ACB}=2R=4$⇒AB=4sin∠ACB=3

解答 解：設△ABC的外接圓的半徑為R，因為$4\overrightarrow{OA}+5\overrightarrow{OB}+6\overrightarrow{OC}=\vec 0$，
所以$4\overrightarrow{OA}+5\overrightarrow{OB}=-6\overrightarrow{OC}$，則16R²+25R²+40R²cos∠AOB=36R²，即8cos∠AOB=-1，
解得：cos∠AOB=-$\frac{1}{8}$．
由2∠ACB=∠AOB，
2cos²∠ACB-1=cos∠AOB=-$\frac{1}{8}$，則cosC=$\frac{\sqrt{7}}{4}$⇒sin∠ACB=$\frac{3}{4}$
由$\frac{AB}{sin∠ACB}=2R=4$⇒AB=4sin∠ACB=3
故答案為：3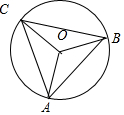

點評 本題考查向量的運算和三角形外心的性質和應用，二倍角公式，解題時要認真審題，仔細解答，注意向量運算法則的靈活運用，屬于中檔題．