Question

13．在平面內，定點A，B，C，D滿足|$\overrightarrow{DA}$|=|$\overrightarrow{DB}$|=|$\overrightarrow{DC}$|，|$\overrightarrow{DA}$|•|$\overrightarrow{DB}$|=|$\overrightarrow{DB}$|•|$\overrightarrow{DC}$|=|$\overrightarrow{DC}$|•|$\overrightarrow{DA}$|=-4，動點P，M滿足|$\overrightarrow{AP}$|=2，$\overrightarrow{PM}$=$\overrightarrow{MC}$，則|$\overrightarrow{BM}$|的最大值是3$\sqrt{2}$+1．

Answer 1

分析 根據條件可知A，B，C三點共圓，M為PC的中點，于是$\overrightarrow{BM}$=$\frac{1}{2}$（$\overrightarrow{BP}+\overrightarrow{BC}$）．建立平面直角坐標系得出$\overrightarrow{BC}，\overrightarrow{BP}$的坐標，計算${\overrightarrow{BM}}^{2}$得出模長關于α的函數，利用三角函數的恒等變換得出模長的最大值．

解答 解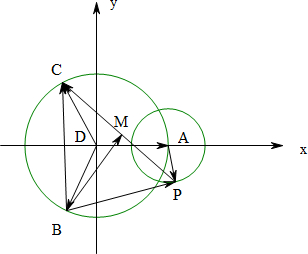：∵|$\overrightarrow{DA}$|=|$\overrightarrow{DB}$|=|$\overrightarrow{DC}$|，∴A，B，C在以D為圓心的圓D上，
∵$\overrightarrow{DA}$•$\overrightarrow{DB}$=$\overrightarrow{DB}$$•\overrightarrow{DC}$=$\overrightarrow{DC}$•$\overrightarrow{DA}$=-4，∴$\overrightarrow{DA}，\overrightarrow{DB}，\overrightarrow{DC}$兩兩夾角相等均為120°，∴|DA|=2$\sqrt{2}$，
以D為原點建立平面直角坐標系，設A（2$\sqrt{2}$，0），則B（-$\sqrt{2}$，-$\sqrt{6}$），C（-$\sqrt{2}$，$\sqrt{6}$），
∴$\overrightarrow{BC}$=（0，2$\sqrt{6}$）．
∵|$\overrightarrow{AP}$|=2，∴P在以A為圓心，以2為半徑的圓A上，
∵$\overrightarrow{PM}$=$\overrightarrow{MC}$，∴M為PC的中點，∴$\overrightarrow{BM}$=$\frac{1}{2}$（$\overrightarrow{BP}+\overrightarrow{BC}$）．
設P（2$\sqrt{2}$+2cosα，2sinα），則$\overrightarrow{BP}$=（3$\sqrt{2}$+2cosα，2sinα+$\sqrt{6}$），
∴$\overrightarrow{BM}$=$\frac{1}{2}$（$\overrightarrow{BP}+\overrightarrow{BC}$）=（cosα+$\frac{3\sqrt{2}}{2}$，sinα+$\frac{3\sqrt{6}}{2}$），
∴${\overrightarrow{BM}}^{2}$=（cosα+$\frac{3\sqrt{2}}{2}$）²+（sinα+$\frac{3\sqrt{6}}{2}$）²=3$\sqrt{2}$cosα+3$\sqrt{6}$sinα+19=6$\sqrt{2}$sin（α+$\frac{π}{6}$）+19，
∴|$\overrightarrow{BM}$|的最大值為$\sqrt{19+6\sqrt{2}}$=$\sqrt{（3\sqrt{2}+1）^{2}}$=3$\sqrt{2}$+1．
故答案為：3$\sqrt{2}$+1

點評 本題主要考查平面向量的應用，根據條件建立坐標系，利用向量與三角函數的綜合問題是解決本題的關鍵．綜合性較強，難度較大．