
【題目】將平面上每個點都以紅、藍兩色之一著色,證明:存在這樣的兩個相似三角形,它們的相似比為1995,并且每一個三角形的三個頂點同色。
【答案】見解析
【解析】
首先證明平面上一定存在三頂點同色的直角三角形.在平面上任作直線![]() ,則
,則![]() 上必有兩點同色,設(shè)此兩點為
上必有兩點同色,設(shè)此兩點為![]() ,
,![]() .過
.過![]() ,
,![]() 分別作
分別作![]() 的垂線
的垂線![]() ,
,![]() .如果
.如果![]() 或
或![]() 上有與
上有與![]() ,
,![]() 同色的點
同色的點![]() ,則
,則
![]() 即為三頂點同色的直角三角形.如果
即為三頂點同色的直角三角形.如果![]() 與
與![]() 上除
上除![]() 與
與![]() 外其余點均與
外其余點均與![]() ,
,![]() 異色,則在
異色,則在![]() 上取異于
上取異于![]() 的兩點
的兩點![]() ,
,![]() ,并過
,并過![]() 作
作![]() ,垂足為
,垂足為![]() ,則
,則![]() 即為三頂點同色的直角三角形.因此,平面上一定存在三頂點同色的直角三角形,設(shè)其中之一為
即為三頂點同色的直角三角形.因此,平面上一定存在三頂點同色的直角三角形,設(shè)其中之一為![]() .將
.將![]() 對稱地補成矩形
對稱地補成矩形![]() .用兩組分別平行于
.用兩組分別平行于![]() 與
與![]() 的
的![]() 等分平行線將矩形
等分平行線將矩形![]() 等分成
等分成![]() 個與原矩形相似的小矩形.(如圖)
個與原矩形相似的小矩形.(如圖)
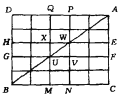
以下用反證法證明:若![]() 為奇數(shù),則在這些小矩形中必有一個,它的頂點中至少有三個同色,即存在一個三頂點同色的小直角三角形.假設(shè)不存在三頂點同色的小直角三角形.線段
為奇數(shù),則在這些小矩形中必有一個,它的頂點中至少有三個同色,即存在一個三頂點同色的小直角三角形.假設(shè)不存在三頂點同色的小直角三角形.線段![]() 上端點及分點共
上端點及分點共![]() 個,
個,![]() 為偶數(shù),因此
為偶數(shù),因此![]() 上必有相鄰的兩點同色(若每相鄰兩點異色,則
上必有相鄰的兩點同色(若每相鄰兩點異色,則![]() ,
,![]() 亦應(yīng)異色,與已知矛盾),不妨設(shè)為
亦應(yīng)異色,與已知矛盾),不妨設(shè)為![]() ,
,![]() .則
.則![]() ,
,![]() 所在的小矩形的另兩個頂點必與
所在的小矩形的另兩個頂點必與![]() ,
,![]() 異色(否則已出現(xiàn)同色小三角形).依次類推,可知矩形
異色(否則已出現(xiàn)同色小三角形).依次類推,可知矩形![]() 中,每條豎線上的兩頂點都同色.同理,線段
中,每條豎線上的兩頂點都同色.同理,線段![]() 上有相鄰兩點
上有相鄰兩點![]() ,
,![]() 同色,也有矩形
同色,也有矩形![]() ,其中每條橫線上的兩頂點都同色.設(shè)矩形
,其中每條橫線上的兩頂點都同色.設(shè)矩形![]() 與
與![]() 的公共部分為小矩形
的公共部分為小矩形![]() ,由以上所說,
,由以上所說,![]() 與
與![]() 同色且
同色且![]() 與
與![]() 同色,從而
同色,從而![]() 即是三頂點同色的小直角三角形.這與假設(shè)矛盾.因此必存在一個三頂點同色的小直角三角形.這個三頂點同色的小直角三角形與原直角三角形是相似的,相似比為
即是三頂點同色的小直角三角形.這與假設(shè)矛盾.因此必存在一個三頂點同色的小直角三角形.這個三頂點同色的小直角三角形與原直角三角形是相似的,相似比為![]() ,當
,當![]() 時就是題目所要證明的結(jié)論.
時就是題目所要證明的結(jié)論.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() 中,
中,![]() 為
為![]() 的中點,
的中點,![]() 為外心,點
為外心,點![]() 滿足
滿足![]() .
.
(1)證明:![]() ;
;
(2)若![]() ,設(shè)
,設(shè)![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() 關(guān)于點
關(guān)于點![]() 對稱,且
對稱,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著城市地鐵建設(shè)的持續(xù)推進,市民的出行也越來越便利,根據(jù)大數(shù)據(jù)統(tǒng)計,某條地鐵線路運行時,發(fā)車時間間隔![]() (單位:分鐘)滿足:
(單位:分鐘)滿足: ![]() ,平均每班地鐵的載客人數(shù)
,平均每班地鐵的載客人數(shù)![]() (單位:人)與發(fā)車時間間隔
(單位:人)與發(fā)車時間間隔![]() 近似地滿足函數(shù)關(guān)系:
近似地滿足函數(shù)關(guān)系: ,
,
(1)若平均每班地鐵的載客人數(shù)不超過1560人,試求發(fā)車時間間隔![]() 的取值范圍;
的取值范圍;
(2)若平均每班地鐵每分鐘的凈收益為![]() (單位:元),則當發(fā)車時間間隔
(單位:元),則當發(fā)車時間間隔![]() 為多少時,平均每班地鐵每分鐘的凈收益最大?并求出最大凈收益.
為多少時,平均每班地鐵每分鐘的凈收益最大?并求出最大凈收益.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某學(xué)校高一學(xué)生有1000名學(xué)生參加一次數(shù)學(xué)小測驗,隨機抽取200名學(xué)生的測驗成績得如圖所示的頻率分布直方圖:

(1)求該學(xué)校高一學(xué)生隨機抽取的200名學(xué)生的數(shù)學(xué)平均成績![]() 和標準差
和標準差![]() (同一組中的數(shù)據(jù)用該組區(qū)間的中點值做代表);
(同一組中的數(shù)據(jù)用該組區(qū)間的中點值做代表);
(2)試估計該校高一學(xué)生在這一次的數(shù)學(xué)測驗成績在區(qū)間![]() 之內(nèi)的概率是多少?測驗成績在區(qū)間
之內(nèi)的概率是多少?測驗成績在區(qū)間![]() 之外有多少位學(xué)生?(參考數(shù)據(jù):
之外有多少位學(xué)生?(參考數(shù)據(jù):![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某果農(nóng)從經(jīng)過篩選(每個水果的大小最小不低于50克,最大不超過100克)的10000個水果中抽取出100個樣本進行統(tǒng)計,得到如下頻率分布表:
級別 | 大小(克) | 頻數(shù) | 頻率 |
一級果 |
| 5 | 0.05 |
二級果 |
|
| |
三級果 |
| 35 |
|
四級果 |
| 30 | |
五級果 |
| 20 | |
合計 | 100 |
請根據(jù)頻率分布表中所提供的數(shù)據(jù),解得下列問題:
(1)求![]() 的值,并完成頻率分布直方圖;
的值,并完成頻率分布直方圖;
(2)若從四級果,五級果中按分層抽樣的方法抽取5個水果,并從中選出2個作為展品,求2個展品中僅有1個是四級果的概率;
(3)若將水果作分級銷售,預(yù)計銷售的價格![]() 元/個與每個水果的大小
元/個與每個水果的大小![]() 克關(guān)系是:
克關(guān)系是: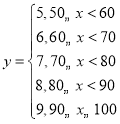 ,則預(yù)計10000個水果可收入多少元?
,則預(yù)計10000個水果可收入多少元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】榆林市政府堅持保護環(huán)境和節(jié)約資源,堅持推進生態(tài)文明建設(shè)。若市財政局下?lián)軐??/span>100百萬元,分別用于植綠護綠和處理污染兩個生態(tài)維護項目,植綠護綠項目五年內(nèi)帶來的生態(tài)收益可表示為投放資金![]() (單位:百萬元)的函數(shù)
(單位:百萬元)的函數(shù)![]() (單位:百萬元):
(單位:百萬元):![]() ,處理污染項目五年內(nèi)帶來的生態(tài)收益可表示為投放資金
,處理污染項目五年內(nèi)帶來的生態(tài)收益可表示為投放資金![]() 單位:(單位:百萬元)的函數(shù)
單位:(單位:百萬元)的函數(shù)![]() (單位:百萬元):
(單位:百萬元):![]() 。
。
(1)設(shè)分配給植綠護綠項目的資金為![]() (百萬元),則兩個生態(tài)項目五年內(nèi)帶來的收益總和為y,寫出y關(guān)于
(百萬元),則兩個生態(tài)項目五年內(nèi)帶來的收益總和為y,寫出y關(guān)于![]() 的函數(shù)解析式和定義域;
的函數(shù)解析式和定義域;
(2)試求出y的最大值,并求出此時對兩個生態(tài)項目的投資分別為多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知A(a,0)、B(0,b)(其中ab≠0)O為坐標原點.
(1)動點P(x,y)滿足![]() ,求P點的軌跡方程;
,求P點的軌跡方程;
(2)設(shè)![]() 是線段AB的n+1(n≥1)等分點,當n=2018時,求
是線段AB的n+1(n≥1)等分點,當n=2018時,求![]() 的值;
的值;
(3)若a=b=1,t∈[0,1],求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 函數(shù)
函數(shù)![]() 為
為![]() 的導(dǎo)函數(shù)
的導(dǎo)函數(shù)
(1)若曲線![]() 與曲線
與曲線![]() 相切,求實數(shù)
相切,求實數(shù)![]() 的值;
的值;
(2)設(shè)函數(shù)![]() 若
若![]() 為函數(shù)
為函數(shù)![]() 的極大值,且
的極大值,且![]()
①求![]() 的值;
的值;
②求證:對于![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給定![]() ,
,![]() ,
,![]() ,
,![]() 所對的邊分別是
所對的邊分別是![]() ,
,![]() ,
,![]() ,在
,在![]() 所在平面作直線
所在平面作直線![]() 與
與![]() 的某兩邊相交,沿
的某兩邊相交,沿![]() 將
將![]() 折成一個空間圖形,將由
折成一個空間圖形,將由![]() 分成的小三角形的不在
分成的小三角形的不在![]() 上的頂點與另一部分的頂點連接,形成一個三棱錐或四棱錐。問:
上的頂點與另一部分的頂點連接,形成一個三棱錐或四棱錐。問:
(1)當![]() 時,
時,![]() 如何作,并折成何種錐體,才能使所得錐體體積最大?(需詳證)
如何作,并折成何種錐體,才能使所得錐體體積最大?(需詳證)
(2)當![]() 時,
時,![]() 如何作,并折成何種錐體,才能使所得錐體體積最大?(敘述結(jié)果,不要證明)
如何作,并折成何種錐體,才能使所得錐體體積最大?(敘述結(jié)果,不要證明)
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com