
已知函數![]() ,記數列
,記數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,當
,當![]() 時,
時,![]()
(1)計算![]() 、
、![]() 、
、![]() 、
、![]() ;
;
(2)猜想![]() 的通項公式,并證明你的結論;
的通項公式,并證明你的結論;
(3)求證:![]() …
…![]()
 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:高中數學 來源: 題型:044
已知函數![]() ,記數列{an}的前n項和為Sn,且有a1=f(1),當n≥2時,
,記數列{an}的前n項和為Sn,且有a1=f(1),當n≥2時,![]() .
.
(1)計算a1,a2,a3,a4;
(2)求出數列{an}的通項公式,并給予證明.
查看答案和解析>>
科目:高中數學 來源:數學教研室 題型:044
(1)計算a1,a2,a3,a4;
(2)求出數列{an}的通項公式,并給予證明.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河南省原名校高三上學期期聯考文科數學試卷(解析版) 題型:解答題
記數列{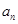 }的前n項和為為
}的前n項和為為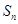 ,且
,且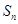 +
+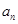 +n=0(n∈N*)恒成立.
+n=0(n∈N*)恒成立.
(1)求證:數列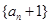 是等比數列;
是等比數列;
(2)已知2是函數f(x)=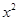 +ax-1的零點,若關于x的不等式f(x)≥
+ax-1的零點,若關于x的不等式f(x)≥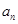 對任意n∈N﹡在x∈(-∞,λ]上恒成立,求實常數λ的取值范圍.
對任意n∈N﹡在x∈(-∞,λ]上恒成立,求實常數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年上海市寶山區高三上學期期末質量監測數學 題型:解答題
已知函數 ,若
,若

 成等差數列.
成等差數列.
(1)求數列 的通項公式;
的通項公式;
(2)設 是不等式
是不等式 整數解的個數,求
整數解的個數,求 ;
;
(3)記數列 的前n項和為
的前n項和為 ,是否存在正數
,是否存在正數 ,對任意正整數
,對任意正整數 ,使
,使 恒成立?若存在,求
恒成立?若存在,求 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源:2011年遼寧名校領航高考預測試(六)數學卷 題型:解答題
(本小題滿分12分)已知函數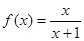 .
.
(Ⅰ)求函數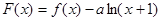 的單調遞增區間;
的單調遞增區間;
(Ⅱ)數列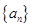 滿足:
滿足: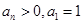 ,且
,且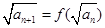 ,記數列
,記數列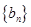 的前n項和為
的前n項和為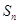 ,
,
且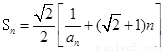 .
.
(ⅰ)求數列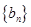 的通項公式;并判斷
的通項公式;并判斷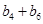 是否仍為數列
是否仍為數列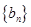 中的項?若是,請證明;否則,說明理由.
中的項?若是,請證明;否則,說明理由.
(ⅱ)設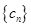 為首項是
為首項是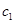 ,公差
,公差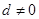 的等差數列,求證:“數列
的等差數列,求證:“數列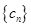 中任意不同兩項之和仍為數列
中任意不同兩項之和仍為數列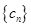 中的項”的充要條件是“存在整數
中的項”的充要條件是“存在整數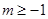 ,使
,使 ”
”
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com