【題目】在某年級的聯歡會上設計了一個摸獎游戲，在一個口袋中裝有3個紅球和7個白球，這些球除顏色外完全相同，一次從中摸出3個球.
（1）設
表示摸出的紅球的個數，求
的分布列和數學期望；
（2）為了提高同學們參與游戲的積極性，參加游戲的同學每人可摸球兩次，每次摸球后放回，若規定兩次共摸出紅球的個數不少于
，且中獎概率大于60%時，即中獎，求
的最大值.
科目：高中數學 來源： 題型：
【題目】設直線l的方程為
，圓O的方程為
．
（1）當m取一切實數時，直線l與圓O都有公共點，求r的取值范圍；
（2）當
時，直線
與圓O交于M，N兩點，若
，求實數t的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司決定對旗下的某商品進行一次評估，該商品原來每件售價為25元，年銷售8萬件.
（1）據市場調查，若價格每提高1元，銷售量將相應減少2000件，要使銷售的總收入不低于原收入，該商品每件定價最多為多少元？
（2）為了抓住2022年冬奧會契機，擴大該商品的影響力，提高年銷售量.公司決定立即對該商品進行全面技術革新和銷售策略改革，并提高定價到
元.公司擬投入
萬作為技改費用，投入50萬元作為固定宣傳費用，投入
萬元作為浮動宣傳費用.試問：當該商品改革后的銷售量
至少達到多少萬件時，才可能使改革后的銷售收入不低于原收入與總投入之和？并求出此時商品的每件定價.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知橢圓
：
的離心率為
，過左焦點
且斜率為
的直線交橢圓于
兩點，線段
的中點為
，直線
：
交橢圓于
兩點.
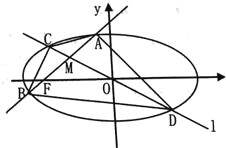
（1）求橢圓的方程；
（2）求證：點在直線上；
（3）是否存在實數，使得
？若存在，求出的值，若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】斜率為k的直線l經過拋物線y＝
x2的焦點F，且與拋物線相交于A，B兩點，若線段|AB|的長為8.
(1)求拋物線的焦點F的坐標和準線方程；
(2)求直線的斜率k.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
.若曲線
在點
處的切線方程為
（
為自然對數的底數）.
（1）求函數
的單調區間；
（2）若關于
的不等式
在（0，+
）上恒成立，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】屠呦呦，第一位獲得諾貝爾科學獎項的中國本土科學家，在2015年獲得諾貝爾生理學或醫學獎，理由是她發現了青蒿素.這種藥品可以有效降低瘧疾患者的死亡率，從青篙中提取的青篙素抗瘧性超強，幾乎達到100%.據監測：服藥后每毫升血液中的含藥量y（微克）與時間t（小時）之間近似滿足如圖所示的曲線．
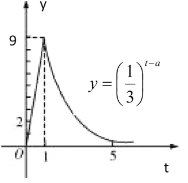
(Ⅰ)寫出服藥一次后y與t之間的函數關系式
；
(Ⅱ)據進一步測定：每毫升血液中含藥量不少于
微克時，治療有效，求服藥一次后治療有效的時間是多長？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在平面直角坐標系
中，平行于
軸且過點
的入射光線
被直線
反射，反射光線
交
軸于
點，圓
過點
，且與、相切．
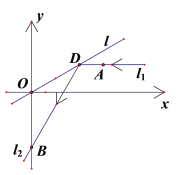
（Ⅰ）求所在直線的方程；
（Ⅱ）求圓的方程．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
