
【題目】如圖,四棱錐![]() 的底面
的底面![]() 是直角梯形,
是直角梯形,![]() ,
, ![]() ,
,![]() ,
,![]() , 且
, 且![]() ,
,![]() ,
,![]()
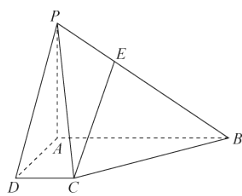
(1)證明:![]() 平面
平面![]() ;
;
(2)求點![]() 到平面
到平面![]() 的距離;
的距離;
【答案】(1)見解析;(2)![]()
【解析】
(1)取![]() 的三等分點
的三等分點![]() ,法一,利用線面平行的判定定理證明.法二,利用面面平行判定定理證明;
,法一,利用線面平行的判定定理證明.法二,利用面面平行判定定理證明;
(2)法一,利用等積轉(zhuǎn)換即![]() ,即可求得,法二,利用空間向量法,求點到面的距離.
,即可求得,法二,利用空間向量法,求點到面的距離.
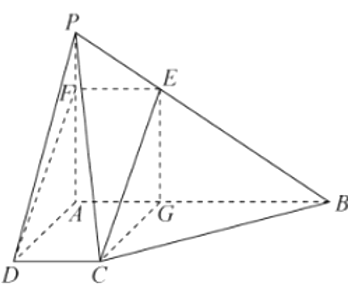
(1)解法一:取![]() 的三等分點
的三等分點![]() ,連結
,連結![]() ,則
,則![]()
又因為![]() ,所以
,所以![]() 且
且![]() ,
,
因為![]() 且
且![]() ,所以
,所以![]() 且
且![]() ,
,
四邊形![]() 是平行四邊形,
是平行四邊形,
所以![]() ,
,
又平面![]() 平面
平面 ![]() ,
,![]() 平面
平面 ![]() ,
,
所以![]() 平面
平面 ![]() .
.
解法二:取![]() 的三等分點
的三等分點![]() ,連結
,連結![]() ,則
,則![]() ,
,
又因為![]() ,
,
所以![]() 且
且![]() ,
,![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
因為![]() 且
且![]() ,所以
,所以![]() 且
且![]() ,
,
四邊形![]() 是平行四邊形.
是平行四邊形.
所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又因為![]() ,
,![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又因為![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解法一:設點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.
因為![]() ,
,![]() ,所以
,所以![]() ,
,
所以,![]() ,因為
,因為![]() ,所以
,所以![]() 平面
平面![]() ,
,
點![]() 平面
平面![]() 的距離是
的距離是![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
因為![]() ,所以,
,所以,![]()
點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.
解法二:設點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.
因為![]() ,
,![]() ,所以
,所以![]()
所以,![]() ,因為
,因為![]() ,所以
,所以![]() 平面
平面![]() ,
,
分別以![]() 為
為![]() 軸
軸![]() 軸
軸![]() 軸,建立空間坐標系,
軸,建立空間坐標系,
![]() ’
’![]() ,
,
設平面![]() 法向量
法向量![]() ,
,
因為 ,所以
,所以![]() ,
,
設![]() 與平面
與平面![]() 所成角為
所成角為![]() , 則
, 則
點![]() 到平面
到平面![]() 的距離
的距離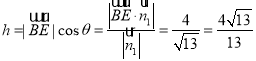 ,
,
點![]() 到平面
到平面![]() 的距離為
的距離為 ![]() .
.


 智趣寒假作業(yè)云南科技出版社系列答案
智趣寒假作業(yè)云南科技出版社系列答案科目:高中數(shù)學 來源: 題型:
【題目】從中國教育在線官方公布的考研動機調(diào)查來看,本科生扎堆考研的原因大概集中在這6個方面:本科就業(yè)壓力大,提升競爭力;通過考研選擇真正感興趣的專業(yè);為了獲得學歷;繼續(xù)深造;隨大流;有名校情結.如圖是2015~2019年全國碩士研究生報考人數(shù)趨勢圖(單位:萬人)的拆線圖.
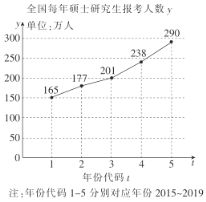
(1)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)根據(jù)(1)中的回歸方程,預測2021年全國碩士研究生報考人數(shù).
參考數(shù)據(jù):![]() ;
;
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為
中斜率和截距的最小二乘估計公式分別為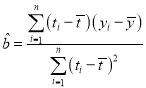 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知直線x=﹣2上有一動點Q,過點Q作直線l,垂直于y軸,動點P在l1上,且滿足![]() (O為坐標原點),記點P的軌跡為C.
(O為坐標原點),記點P的軌跡為C.
(1)求曲線C的方程;
(2)已知定點M(![]() ,0),N(
,0),N(![]() ,0),點A為曲線C上一點,直線AM交曲線C于另一點B,且點A在線段MB上,直線AN交曲線C于另一點D,求△MBD的內(nèi)切圓半徑r的取值范圍.
,0),點A為曲線C上一點,直線AM交曲線C于另一點B,且點A在線段MB上,直線AN交曲線C于另一點D,求△MBD的內(nèi)切圓半徑r的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨著“北京八分鐘”在韓國平昌冬奧會驚艷亮相,冬奧會正式進入了北京周期,全社會對冬奧會的熱情空前高漲.
(1)為迎接冬奧會,某社區(qū)積極推動冬奧會項目在社區(qū)青少年中的普及,并統(tǒng)計了近五年來本社區(qū)冬奧項目青少年愛好者的人數(shù)![]() (單位:人)與時間
(單位:人)與時間![]() (單位:年),列表如下:
(單位:年),列表如下:

依據(jù)表格給出的數(shù)據(jù),是否可用線性回歸模型擬合![]() 與
與![]() 的關系,請計算相關系數(shù)
的關系,請計算相關系數(shù)![]() 并加以說明(計算結果精確到0.01).
并加以說明(計算結果精確到0.01).
(若![]() ,則線性相關程度很高,可用線性回歸模型擬合)
,則線性相關程度很高,可用線性回歸模型擬合)
附:相關系數(shù)公式 ,參考數(shù)據(jù)
,參考數(shù)據(jù)![]() .
.
(2)某冰雪運動用品專營店為吸引廣大冰雪愛好者,特推出兩種促銷方案.
方案一:每滿600元可減100元;
方案二:金額超過600元可抽獎三次,每次中獎的概率同為![]() ,且每次抽獎互不影響,中獎1次打9折,中獎2次打8折,中獎3次打7折. v
,且每次抽獎互不影響,中獎1次打9折,中獎2次打8折,中獎3次打7折. v
兩位顧客都購買了1050元的產(chǎn)品,并且都選擇第二種優(yōu)惠方案,求至少有一名顧客比選擇方案一更優(yōu)惠的概率;
②如果你打算購買1000元的冰雪運動用品,請從實際付款金額的數(shù)學期望的角度分析應該選擇哪種優(yōu)惠方案.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】微信是現(xiàn)代生活信息交流的重要工具,隨機對使用微信的![]() 人進行統(tǒng)計,得到如下數(shù)據(jù)統(tǒng)計表,每天使用微信時間在兩小時以上的人被定義為“微信依賴”,不超過
人進行統(tǒng)計,得到如下數(shù)據(jù)統(tǒng)計表,每天使用微信時間在兩小時以上的人被定義為“微信依賴”,不超過![]() 兩小時的人被定義為“非微信依賴”,已知“非微信依賴”與“微信依賴”人數(shù)比恰為
兩小時的人被定義為“非微信依賴”,已知“非微信依賴”與“微信依賴”人數(shù)比恰為![]() .
.
使用微信時間(單位:小時) | 頻數(shù) | 頻率 |
| 5 | 0.05 |
| 15 | 0.15 |
| 15 | 0.15 |
|
|
|
| 30 | 0.30 |
|
|
|
合計 | 100 | 1.00 |
(1)確定![]() 的值;
的值;
(2)為進一步了解使用微信對自己的日常工作和生活是否有影響,從“微信依賴”和“非微信依賴”![]() 人中用分層抽樣的方法確定
人中用分層抽樣的方法確定![]() 人,若需從這
人,若需從這![]() 人中隨機選取
人中隨機選取![]() 人進行問卷調(diào)查,設選取的
人進行問卷調(diào)查,設選取的![]() 人中“微信依賴”的人數(shù)為
人中“微信依賴”的人數(shù)為![]() ,求
,求![]() 的分布列;
的分布列;
(3)求選取的![]() 人中“微信依賴”至少
人中“微信依賴”至少![]() 人的概率.
人的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】華羅庚中學高二排球隊和籃球隊各有10名同學,現(xiàn)測得排球隊10人的身高(單位:![]() )分別是:162、170、171、182、163、158、179、168、183、168,籃球隊10人的身高(單位:
)分別是:162、170、171、182、163、158、179、168、183、168,籃球隊10人的身高(單位:![]() )分別是:170、159、162、173、181、165、176、168、178、179.
)分別是:170、159、162、173、181、165、176、168、178、179.
(1)請根據(jù)兩隊身高數(shù)據(jù)作出莖葉圖,并分析指出哪個隊的身高數(shù)據(jù)方差較小(無需計算)以及排球隊的身高數(shù)據(jù)的中位數(shù)與眾數(shù);
(2)現(xiàn)從兩隊所有身高超過![]() 的同學中隨機抽取三名同學,則恰好兩人來自排球隊一人來自籃球隊的概率是多少?
的同學中隨機抽取三名同學,則恰好兩人來自排球隊一人來自籃球隊的概率是多少?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】小明下班回家途經(jīng)3個有紅綠燈的路口,交通法規(guī)定:若在路口遇到紅燈,需停車等待;若在路口沒遇到紅燈,則直接通過.經(jīng)長期觀察發(fā)現(xiàn):他在第一個路口遇到紅燈的概率為![]() ,在第二、第三個道口遇到紅燈的概率依次減小,在三個道口都沒遇到紅燈的概率為
,在第二、第三個道口遇到紅燈的概率依次減小,在三個道口都沒遇到紅燈的概率為![]() ,在三個道口都遇到紅燈的概率為
,在三個道口都遇到紅燈的概率為![]() ,且他在各路口是否遇到紅燈相互獨立.
,且他在各路口是否遇到紅燈相互獨立.
(1)求小明下班回家途中至少有一個道口遇到紅燈的概率;
(2)求小明下班回家途中在第三個道口首次遇到紅燈的概率;
(3)記![]() 為小明下班回家途中遇到紅燈的路口個數(shù),求數(shù)學期望
為小明下班回家途中遇到紅燈的路口個數(shù),求數(shù)學期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]()
![]() 中,對任何正整數(shù)n都有:
中,對任何正整數(shù)n都有: ![]()
(1)若數(shù)列![]() 是首項和公差都是1的等差數(shù)列,求證:數(shù)列
是首項和公差都是1的等差數(shù)列,求證:數(shù)列![]() 是等比數(shù)列;
是等比數(shù)列;
(2)若數(shù)列![]() 是首項為1的等比數(shù)列,數(shù)列
是首項為1的等比數(shù)列,數(shù)列![]() 是否是等差數(shù)列?若是請求出通項公式.
是否是等差數(shù)列?若是請求出通項公式.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com