【題目】某種產品的廣告費用支出x(萬元)與銷售額y(萬元)之間有如下的對應數據：
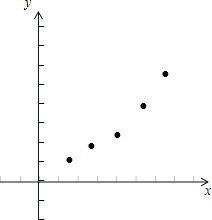
(1)畫出散點圖；
(2)求回歸直線方程；
(3)據此估計廣告費用為9萬元時，銷售收入y的值.
注：①參考公式：線性回歸方程系數公式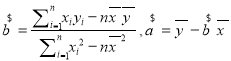
；
②參考數據：
【答案】（1）詳見解析（2）y=6.5x+17.5（3）當x=9時，預報y的值為y=76
【解析】
（1）根據表中所給的五對數據，得到五個有序數對，在平面直角坐標系中畫出點，得到散點圖．
（2）先做出橫標和縱標的平均數，得到這組數據的樣本中心點，利用最小二乘法做出線性回歸方程的系數，再做出a的值，協會粗線性回歸方程．
（3）把所給的x的值代入線性回歸方程，求出y的值，這里的y的值是一個預報值，或者說是一個估計值．
解：（1）根據表中所給的五對數據，得到五個有序數對，在平面直角坐標系中畫出點，得到散點圖．
（2）∵
=5，
=50
∴
=
=6.5
∴
=-b=50-6.5×5=17.5
∴回歸直線方程為y=6.5x+17.5
（3）當x=9時，預報y的值為y=9×6.5+17.5=76．
第三學期贏在暑假系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案科目：高中數學 來源： 題型：
【題目】某個體經營者把開始六個月試銷A、B兩種商品的逐月投資與所獲純利潤列成下表：
投資A商品金額（萬元） | 1 | 2 | 3 | 4 | 5 | 6 |
獲純利潤（萬元） | 0.65 | 1.39 | 1.85 | 2 | 1.84 | 1.40 |
投資B商品金額（萬元） | 1 | 2 | 3 | 4 | 5 | 6 |
獲純利潤（萬元） | 0.25 | 0.49 | 0.76 | 1 | 1.26 | 1.51 |
該經營者準備下月投入12萬元經營這兩種產品，但不知投入A、B兩種商品各多少才最合算．請你幫助制定一下資金投入方案，使得該經營者能獲得最大利潤，并按你的方案求出該經營者下月可獲得的最大利潤（結果保留兩個有效數字）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下面是追蹤調查200個某種電子元件壽命（單位:
)頻率分布直方圖，如圖：
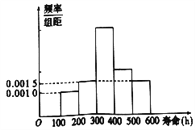
其中300-400、400-500兩組數據丟失，下面四個說法中有且只有一個與原數據相符，這個說法是( )
①壽命在300-400的頻數是90；
②壽命在400-500的矩形的面積是0.2；
③用頻率分布直方圖估計電子元件的平均壽命為：
④壽命超過
的頻率為0.3
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列隨機事件：
①某射手射擊一次，可能命中
環，
環，
環，
，
環；
②一個小組有男生
人，女生
人，從中任選人進行活動匯報；
③一只使用中的燈泡壽命長短；
④拋出一枚質地均勻的硬幣，觀察其出現正面或反面的情況；
⑤中秋節前夕，某市有關部門調查轄區內某品牌的月餅質量，給該品牌月餅評“優”或“差”.
這些事件中，屬于古典概型的是________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在古代，直角三角形中較短的直角邊稱為“勾”,較長的直角邊稱為“股”，斜邊稱為“弦”.三國時期吳國數學家趙爽用“弦圖”( 如圖) 證明了勾股定理，證明方法敘述為:“按弦圖,又可以勾股相乘為朱實二，倍之為朱實四，以勾股之差自相乘為中黃實，加差實，亦成弦實.”這里的“實”可以理解為面積.這個證明過程體現的是這樣一個等量關系:“兩條直角邊的乘積是兩個全等直角三角形的面積的和(朱實二 )，4個全等的直角三角形的面積的和(朱實四) 加上中間小正方形的面積(黃實) 等于大正方形的面積(弦實)”. 若弦圖中“弦實”為16，“朱實一”為
,現隨機向弦圖內投入一粒黃豆(大小忽略不計)，則其落入小正方形內的概率為( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，三棱柱
的各棱長均為2， 
面
，E，F分別為棱
的中點．
（1）求證：直線BE∥平面
；
（2）平面
與直線AB交于點M，指出點M的位置，說明理由，并求三棱錐
的體積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
