
【題目】已知函數![]() (a為常數)的圖象與
(a為常數)的圖象與![]() 軸交于點
軸交于點![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線斜率為
處的切線斜率為![]()
(1)求![]() 的值及函數
的值及函數![]() 的極值;
的極值;
(2)證明:當![]() 時,
時,![]()
【答案】(1)當x=ln2時,f(x)取得極小值,且極小值為f(ln2)=2-ln4,f(x)無極大值.(2)見解析
【解析】試題分析:(1)首先求點![]() 的坐標
的坐標![]() ,再根據
,再根據![]() ,解得
,解得![]() 的值,然后求
的值,然后求![]() 的
的![]() 值,以及兩側的單調性,根據單調性求得函數的極值;(2)設函數
值,以及兩側的單調性,根據單調性求得函數的極值;(2)設函數![]() ,根據(1)的結果可知函數單調遞增,即證
,根據(1)的結果可知函數單調遞增,即證![]() .
.
試題解析: (1)由f(x)=ex-ax,得f′(x)=ex-a. 又f′(0)=1-a=-1,得a=2.
所以f(x)=ex-2x,f′(x)=ex-2. 令f′(x)=0,得x=ln2.
當x<ln2時,f′(x)<0,f(x)單調遞減;當x>ln2時,f′(x)>0,f(x)單調遞增.
所以當x=ln2時,f(x)取得極小值,且極小值為f(ln2)=eln2-2ln2=2-ln4,f(x)無極大值.
(2)令g(x)=ex-x2,則g′(x)=ex-2x. 由(1)得g′(x)=f(x)≥f(ln2)>0,
故g(x)在R上單調遞增,又g(0)=1>0,因此,當x>0時,g(x)>g(0)>0,即x2<ex.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() 是奇函數.
是奇函數.
![]() 求實數m,n的值;
求實數m,n的值;
![]() 若函數
若函數![]() 的定義域為
的定義域為![]() 判斷函數
判斷函數![]() 的單調性,并用定義證明;
的單調性,并用定義證明;![]() 是否存在實數t,使得關于x的不等式
是否存在實數t,使得關于x的不等式![]() 在
在![]() 上有解?若存在,求出t的取值范圍;若不存在,說明理由.
上有解?若存在,求出t的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C是圓周上不同于A,B的任意一點,PA⊥平面ABC,則四面體P-ABC的四個面中,直角三角形的個數有( )

A. 4個B. 3個C. 2個D. 1個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga(x+1)﹣loga(1﹣x),a>0且a≠1.
(1)求f(x)的定義域;
(2)判斷f(x)的奇偶性并予以證明;
(3)當a>1時,求使f(x)>0的x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在R上的奇函數,當
是定義在R上的奇函數,當![]() 時,
時,![]() .
.
(Ⅰ)求函數![]() 在R上的解析式;
在R上的解析式;
(Ⅱ)若![]() ,函數
,函數![]() ,是否存在實數m使得
,是否存在實數m使得![]() 的最小值為
的最小值為![]() ,若存在,求m的值;若不存在,請說明理由.
,若存在,求m的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場舉行有獎促銷活動,顧客購買一定金額商品后即可抽獎,每次抽獎都從裝有4個紅球、6個白球的甲箱和裝有5個紅球、5個白球的乙箱中,各隨機摸出1個球,在摸出的2個球中,若都是紅球,則獲一等獎;若只有1個紅球,則獲二等獎;若沒有紅球,則不獲獎.
(1)求顧客抽獎1次能獲獎的概率;
(2)若某顧客有3次抽獎機會,記該顧客在3次抽獎中獲一等獎的次數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列{an}中,已知a1=2,an+1=3an+2n﹣1.
(1)求證:數列{an+n}為等比數列;
(2)記bn=an+(1﹣λ)n,且數列{bn}的前n項和為Tn , 若T3為數列{Tn}中的最小項,求λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面五邊形![]() 是軸對稱圖形(如圖1),BC為對稱軸,AD⊥CD,AD=AB=1,
是軸對稱圖形(如圖1),BC為對稱軸,AD⊥CD,AD=AB=1,![]() ,將此五邊形沿BC折疊,使平面ABCD⊥平面BCEF,得到如圖2所示的空間圖形,對此空間圖形解答下列問題.
,將此五邊形沿BC折疊,使平面ABCD⊥平面BCEF,得到如圖2所示的空間圖形,對此空間圖形解答下列問題.
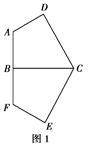
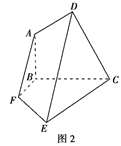
(1)證明:AF∥平面DEC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com