
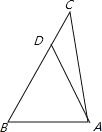
【題目】在![]() 中,
中,![]() ,則
,則![]() ____________.
____________.
【答案】![]()
【解析】
根據余弦定理化簡![]() ,得到
,得到![]() ;由題意,在BC上取D,使得BD=AD,連接AD,找出A﹣B,設BD=x,在△ADC中兩次利用余弦定理將cos(A﹣B)及cosC表示出,分別求出x建立關于a,b的方程,化簡變形后利用整體換元求出答案.
;由題意,在BC上取D,使得BD=AD,連接AD,找出A﹣B,設BD=x,在△ADC中兩次利用余弦定理將cos(A﹣B)及cosC表示出,分別求出x建立關于a,b的方程,化簡變形后利用整體換元求出答案.
由題意知,![]() 4cosC,
4cosC,
∴由余弦定理得,![]() 4
4![]() ,
,
化簡可得![]() =2
=2![]() ,則
,則![]() ,
,
又![]() 中不妨設a>b,∴A>B.在BC上取D,使得BD=AD,連接AD,
中不妨設a>b,∴A>B.在BC上取D,使得BD=AD,連接AD,
設BD=x,則AD=x,DC=a﹣x,AC=b,
在△ADC中, cos∠DAC=cos(A﹣B)![]() ,
,
由余弦定理得:(a﹣x)2=x2+b2﹣2xb![]() ,
,
即:(b﹣6a)x=![]() ,
,
解得:x=![]() .①
.①
又在△ADC中,由余弦定理還可得cosC![]() ,
,
∴cosC![]() ,化簡得x=
,化簡得x=![]() ,②
,②
由①②可得![]() ,又
,又![]() =2
=2![]() ,
,
聯立可得![]() =
=![]() ,即
,即![]() =
=![]() ,
,
兩邊同時除以![]() ,得
,得![]() =
=![]() +6,令
+6,令![]() ,則12
,則12![]() ,解得t=
,解得t=![]() 或
或![]() ,
,
又由題意![]() ,∴t=cosC
,∴t=cosC![]() =
=![]() ,
,
故答案為:![]() .
.


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:高中數學 來源: 題型:
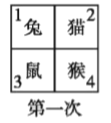
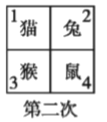
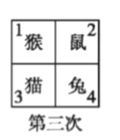
【題目】四個小動物換座位,開始是鼠、猴、兔、貓分別坐在 1,2,3,4 號位子上(如圖), 第一次前后排動物互換座位,第二次左右列動物互換座位,.....,這樣交替進行下去,那么第 2013 次互換座位后,小兔的座位對應的是( )

A. 編號 1 B. 編號 2 C. 編號 3 D. 編號 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一個圓錐的底面半徑為1,高為3,在圓錐中有一個半徑為x的內接圓柱.

(1)試用x表示圓柱的高;
(2)當x為何值時,圓柱的側面積最大,最大側面積是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據調查,某地區有300萬從事傳統農業的農民,人均年收入6000元,為了增加農民的收入,當地政府積極引進資本,建立各種加工企業,對當地的農產品進行深加工,同時吸收當地部分農民進入加工企業工作,據估計,如果有![]() 萬人進企業工作,那么剩下從事傳統農業的農民的人均年收入有望提高
萬人進企業工作,那么剩下從事傳統農業的農民的人均年收入有望提高![]() ,而進入企業工作的農民的人均年收入為
,而進入企業工作的農民的人均年收入為![]() 元.
元.
(1)在建立加工企業后,多少農民進入企業工作,能夠使剩下從事傳統農業農民的總收入最大,并求出最大值;
(2)為了保證傳統農業的順利進行,限制農民加入加工企業的人數不能超過總人數的![]() ,當地政府如何引導農民,即
,當地政府如何引導農民,即![]() 取何值時,能使300萬農民的年總收入最大.
取何值時,能使300萬農民的年總收入最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校有![]() ,
,![]() ,
,![]() ,
,![]() 四件作品參加航模類作品比賽.已知這四件作品中恰有兩件獲獎.在結果揭曉前,甲、乙、丙、丁四位同學對這四件參賽作品的獲獎情況預測如下:
四件作品參加航模類作品比賽.已知這四件作品中恰有兩件獲獎.在結果揭曉前,甲、乙、丙、丁四位同學對這四件參賽作品的獲獎情況預測如下:
甲說:“![]() 、
、![]() 同時獲獎”;
同時獲獎”;
乙說:“![]() 、
、![]() 不可能同時獲獎”;
不可能同時獲獎”;
丙說:“![]() 獲獎”;
獲獎”;
丁說:“![]() 、
、![]() 至少一件獲獎”.
至少一件獲獎”.
如果以上四位同學中有且只有二位同學的預測是正確的,則獲獎的作品是( )
A. 作品![]() 與作品
與作品![]() B. 作品
B. 作品![]() 與作品
與作品![]() C. 作品
C. 作品![]() 與作品
與作品![]() D. 作品
D. 作品![]() 與作品
與作品![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在下列命題中,①![]() 的一個充要條件是
的一個充要條件是![]() 與它的共軛復數相等:
與它的共軛復數相等:
②利用獨立性檢驗來考查兩個分類變量![]() ,
,![]() 是否有關系,當隨機變量
是否有關系,當隨機變量![]() 的觀測值
的觀測值![]() 值越大,“
值越大,“![]() 與
與![]() 有關系”成立的可能性越大;
有關系”成立的可能性越大;
③在回歸分析模型中,若相關指數越大,則殘差平方和越小,模型的擬合效果越好;
④若![]() ,
,![]() 是兩個相等的實數,則
是兩個相等的實數,則![]() 是純虛數;
是純虛數;
⑤某校高三共有![]() 個班,
個班,![]() 班有
班有![]() 人,
人,![]() 班有
班有![]() 人,
人,![]() 班有
班有![]() 人,由此推測各班都超過
人,由此推測各班都超過![]() 人,這個推理過程是演繹推理.
人,這個推理過程是演繹推理.
其中真命題的序號為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,直線l:
,直線l:![]() ,設圓C的半徑為1,圓心在l上.
,設圓C的半徑為1,圓心在l上.
![]() 若圓心C也在直線
若圓心C也在直線![]() 上,過A作圓C的切線,求切線方程;
上,過A作圓C的切線,求切線方程;
![]() 若圓C上存在點M,使
若圓C上存在點M,使![]() ,求圓心C的橫坐標a取值范圍.
,求圓心C的橫坐標a取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com