【題目】某商場舉行有獎促銷活動，顧客購買一定金額商品后即可抽獎，每次抽獎都從裝有4個紅球、6個白球的甲箱和裝有5個紅球、5個白球的乙箱中，各隨機摸出1個球，在摸出的2個球中，若都是紅球，則獲一等獎；若只有1個紅球，則獲二等獎；若沒有紅球，則不獲獎.
（1）求顧客抽獎1次能獲獎的概率；
（2）若某顧客有3次抽獎機會，記該顧客在3次抽獎中獲一等獎的次數為
，求的分布列和數學期望.
【答案】（1）
；（2）詳見解析.
【解析】
試題分析：（1）記事件
｛從甲箱中摸出的1個球是紅球｝，
｛從乙箱中摸出的1個球是紅球｝
｛顧客抽獎1次獲一等獎｝，
｛顧客抽獎1次獲二等獎｝，
｛顧客抽獎1次能獲獎｝，則可知
與
相互獨立，
與
互斥，
與
互斥，且
，
，
，再
利用概率的加法公式即可求解；（2）分析題意可知
，分別求得
，
，
，
，即可知
的概率分布及其期望.
試題解析：（1）記事件｛從甲箱中摸出的1個球是紅球｝，｛從乙箱中摸出的1個球是紅球｝
｛顧客抽獎1次獲一等獎｝，｛顧客抽獎1次獲二等獎｝，｛顧客抽獎1次能獲獎｝，由題意，與相互獨立，與互斥，與互斥，且，，，
∵
，
，∴
，
，故所求概率為
；（2）顧客抽獎3次獨立重復試驗，由（1）知，顧客抽獎1次獲一等獎的概率為
，∴，
于是，，，
，故
的分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
的數學期望為 
.
名校名師培優作業本加核心試卷系列答案
全程金卷系列答案科目：高中數學 來源： 題型：
【題目】甲、乙、丙三臺機床各自獨立地加工同一種零件，已知甲機床加工的零件是一等品而乙機床加工的零件不是一等品的概率是
，乙機床加工的零件是一等品而丙機床加工的零件不是一等品的概率是
，甲、乙兩臺機床加工的零件都是一等品的概率是
.
（1）分別求甲、乙、丙三臺機床各自加工的零件是一等品的概率；
（2）從甲、乙、丙三臺機床加工的零件中各取一個檢驗，求至少有一個一等品的概率；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
經過點
， 
，并且直線
平分圓.
（1）求圓的方程；
（2）若直線
與圓交于
兩點，是否存在直線
，使得
（
為坐標原點），若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】7人站成一排.（寫出必要的過程，結果用數字作答）
（1）甲、乙兩人相鄰的排法有多少種？
（2）甲、乙兩人不相鄰的排法有多少種？
（3）甲、乙、丙三人兩兩不相鄰的排法有多少種？
（4）甲、乙、丙三人至多兩人不相鄰的排法有多少種？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨機抽取了40輛汽車在經過路段上某點是的車速（
），現將其分成六段：
，
后得到如圖所示的頻率分布直方圖.
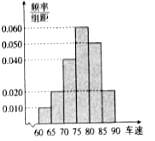
（I）現有某汽車途經該點，則其速度低于80
的概率約是多少？
（II）根據頻率分布直方圖，抽取的40輛汽車經過該點的平均速度是多少？
（III）在抽取的40輛汽車且速度在
（）內的汽車中任取2輛，求這2輛車車速都在
（）內的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】長時間用手機上網嚴重影響著學生的身體健康，某校為了解
兩班學生手機上網的時長，分別從這兩個班中隨機抽取5名同學進行調查，將他們平均每周手機上網的時長作為樣本，繪制成莖葉圖如圖所示（圖中莖葉表示十位數字，葉表示個位數字）．
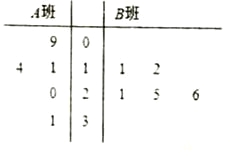
（1）分別求出圖中所給兩組樣本數據的平均值，并據此估計，哪個班的學生平均上網時間較長；
（2）從
班的樣本數據中隨機抽取一個不超過19的數據記為
，從
班的樣本數據中隨機抽取一個不超過21的數據記為
，求
的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系
中，設傾斜角為
的直線
的參數方程為
（
為參數）與曲線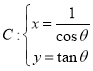
（
為參數）相交于不同的兩點
．
（1）若
，求線段
的中點的直角坐標；
（2）若直線
的斜率為2，且過已知點
，求
的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
