
【題目】4月23日是世界讀書日,為提高學生對讀書的重視,讓更多的人暢游于書海中,從而收獲更多的知識,某高中的校學生會開展了主題為“讓閱讀成為習慣,讓思考伴隨人生”的實踐活動,校學生會實踐部的同學隨即抽查了學校的40名高一學生,通過調查它們是喜愛讀紙質書還是喜愛讀電子書,來了解在校高一學生的讀書習慣,得到如表列聯表:
喜歡讀紙質書 | 不喜歡讀紙質書 | 合計 | |
男 | 16 | 4 | 20 |
女 | 8 | 12 | 20 |
合計 | 24 | 16 | 40 |
(Ⅰ)根據如表,能否有99%的把握認為是否喜歡讀紙質書籍與性別有關系?
(Ⅱ)從被抽查的16名不喜歡讀紙質書籍的學生中隨機抽取2名學生,求抽到男生人數ξ的分布列及其數學期望E(ξ).
參考公式:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下列的臨界值表供參考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案科目:高中數學 來源: 題型:
【題目】下列敘述正確的個數是( )
①若a>b,則ac2>bc2;
②若命題p為真命題題,命題q為假命題,則p∨q為假命題;
③若命題p:x0∈R,x ![]() ﹣x0+1≤0,則¬p:x∈R,x2﹣x+1>0.
﹣x0+1≤0,則¬p:x∈R,x2﹣x+1>0.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C的對邊分別為a,b,c,已知2ccosA+a=2b
(1)求角C的值;
(2)若c=2,且△ABC的面積為 ![]() ,求a,b.
,求a,b.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的三個內角A,B,C所對的邊分別是a,b,c,B是鈍角,且 ![]() a=2bsinA.
a=2bsinA.
(1)求B的大小;
(2)若△ABC的面積為 ![]() ,且b=7,求a+c的值;
,且b=7,求a+c的值;
(3)若b=6,求△ABC面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c分別是△ABC的三個內角A,B,C所對的邊,且滿足(2b﹣a)cosC=ccosA.
(Ⅰ)求角C的大小;
(Ⅱ)設![]() ,求y的最大值并判斷當y取得最大值時△ABC的形狀.
,求y的最大值并判斷當y取得最大值時△ABC的形狀.
查看答案和解析>>
科目:高中數學 來源: 題型:
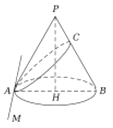
【題目】2000多年前,古希臘大數學家阿波羅尼奧斯((Apollonius)發現:平面截圓錐的截口曲線是圓錐曲線.已知圓錐的高為![]() ,
, ![]() 為地面直徑,頂角為
為地面直徑,頂角為![]() ,那么不過頂點
,那么不過頂點![]() 的平面;與
的平面;與![]() 夾角
夾角![]() 時,截口曲線為橢圓;與
時,截口曲線為橢圓;與![]() 夾角
夾角![]() 時,截口曲線為拋物線;與
時,截口曲線為拋物線;與![]() 夾角
夾角![]() 時,截口曲線為雙曲線.如圖,底面內的直線
時,截口曲線為雙曲線.如圖,底面內的直線![]() ,過
,過![]() 的平面截圓錐得到的曲線為橢圓,其中與
的平面截圓錐得到的曲線為橢圓,其中與![]() 的交點為
的交點為![]() ,可知
,可知![]() 為長軸.那么當
為長軸.那么當![]() 在線段
在線段![]() 上運動時,截口曲線的短軸頂點的軌跡為( )
上運動時,截口曲線的短軸頂點的軌跡為( )
A. 圓的部分 B. 橢圓的部分 C. 雙曲線的部分 D. 拋物線的部分
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系,已知曲線
軸正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為:
的極坐標方程為: ![]() ,直線
,直線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數,
為參數, ![]() ).
).
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 交于兩點
交于兩點![]() ,且線段
,且線段![]() 的中點為
的中點為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設△ABC的內角A,B,C的對邊分別為a,b,c,已知4sinA=4cosBsinC+bsin2C,且C≠ ![]() .
.
(1)求c;
(2)若C= ![]() ,求△ABC周長的取值范圍.
,求△ABC周長的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com