
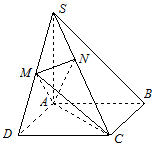
 如圖,在四棱錐S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,點M是SD的中點,AN⊥SC,且交SC于點N.
如圖,在四棱錐S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,點M是SD的中點,AN⊥SC,且交SC于點N.分析 (Ⅰ)連結BD交AC于E,連結ME,推導出ME∥SB,由此能證明SB∥平面ACM.
(Ⅱ)推導出CN為點C到平面AMN的距離,由此能求出點C到平面AMN的距離.
解答 證明:(Ⅰ)連結BD交AC于E,連結ME.
∵ABCD是正方形,∴E是BD的中點.
∵M是SD的中點,∴ME是△DSB的中位線.
∴ME∥SB. …(3分)
又∵ME?平面ACM,SB?平面ACM,
∴SB∥平面ACM. …(5分)
解:(Ⅱ)由條件有DC⊥SA,DC⊥DA,
∴DC⊥平面SAD,∴AM⊥DC.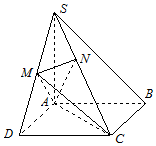
又∵SA=AD,M是SD的中點,∴AM⊥SD.
∴AM⊥平面SDC.∴SC⊥AM.…(8分)
由已知SC⊥AN,∴SC⊥平面AMN.
于是CN⊥面AMN,則CN為點C到平面AMN的距離 …(9分)
在Rt△SAC中,$SA=2,AC=2\sqrt{2},SC=\sqrt{S{A^2}+A{C^2}}=2\sqrt{3}$,
于是$A{C^2}=CN•SC⇒CN=\frac{{4\sqrt{3}}}{3}$
∴點C到平面AMN的距離為$\frac{{4\sqrt{3}}}{3}$. …(12分)
點評 本題考查線面平行的證明,考查點到直線的距離求法,是中檔題,解題時要認真審題,注意空間思維能力的培養.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{1+\sqrt{5}}}{2}$ | B. | $\frac{{3+\sqrt{5}}}{4}$ | C. | $\sqrt{\frac{{1+\sqrt{5}}}{2}}$ | D. | $\frac{{\sqrt{3+\sqrt{5}}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3π}{10}$ | B. | $\frac{π}{20}$ | C. | $\frac{3π}{20}$ | D. | $\frac{π}{10}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 215° | B. | 225° | C. | 235° | D. | 245° |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com