
分析 (1)先確定函數f(x)的定義域,然后對函數f(x)求導,根據導函數大于0時原函數單調遞增,導函數小于0時原函數單調遞減求出單調區間.
(2)分別表示出函數h(x)=-f(x)、g(x)的值域,根據f(x)的值域應為g(x)的值域的子集可得答案.
解答 解:(1)f(x)=lnx-ax,
∴x>0,即函數f(x)的定義域為(0,+∞)
∴當a≤0時,f(x)在(0,+∞)上是增函數
當a>0時,∵f'(x)=$\frac{1}{x}$-a=$\frac{1-ax}{x}$,
∵f′(x)>0,則1-ax>0,ax<1,x<$\frac{1}{a}$,f′(x)<0,則1-ax<0,ax>1,
x>$\frac{1}{a}$即當a>0時f(x)在(0,$\frac{1}{a}$)上是增函數,在($\frac{1}{a}$,+∞)上是減函數.
(2)則由已知,對于任意的x1∈(1,2),總存在x2∈(1,2),
使-f(x1)=g(x2),
設h(x)=-f(x)在(1,2)的值域為A,g(x)在(1,2)的值域為B,
得A⊆B
由(1)知a=1時,h′(x)=$\frac{1-x}{x}$<0在(1,2)1上是減函數,
∴h(x)在x∈(1,2)上單調遞減,
∴h(x)的值域為A=(ln2-2,-1)
∵g'(x)=bx2-b=b(x-1)(x+1)
∴(i)當b<0時,g(x)在(1,2)上是減函數,
此時,g(x)的值域為B=($\frac{2}{3}$b,-$\frac{2}{3}$b)
為滿足A⊆B,又-$\frac{2}{3}$b≥0>-1
∴$\frac{2}{3}$b≤ln2-2.即b≤$\frac{3}{2}$ln2-3.
(ii)當b>0時,g(x)在(1,2)上是單調遞增函數,
此時,g(x)的值域為B=(-$\frac{2}{3}$b,$\frac{2}{3}$b)
為滿足A⊆B,又$\frac{2}{3}$b≥0>-1.
∴-$\frac{2}{3}$b≤ln2-2
∴b≥-$\frac{3}{2}$(ln2-2)=3-$\frac{3}{2}$ln2,
綜上可知b的取值范圍是(-∞,$\frac{3}{2}$ln2-3]∪[3-$\frac{3}{2}$ln2,+∞).
點評 本題主要考查函數單調性與其導函數的正負之間的關系,即當導函數大于0時原函數單調遞增,當導函數小于0時原函數單調遞減.


 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | ($\frac{3}{2},6$) | B. | ($\frac{3}{2},2$) | C. | (1,6) | D. | (1,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ($\frac{1}{3}$,1) | B. | [1,4] | C. | ($\frac{1}{3}$,4] | D. | [1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
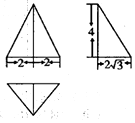
| A. | $\frac{{64\sqrt{3}}}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{{32\sqrt{3}}}{3}$ | D. | $\frac{32}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com