
【題目】設函數![]() .
.
(1)若![]() ,討論
,討論![]() 的單調性;
的單調性;
(2)求正實數![]() 的值,使得
的值,使得![]() 為
為![]() 的一個極值.
的一個極值.
【答案】(1)![]() 在
在![]() 單調遞增.
單調遞增.
(2)![]() .
.
【解析】分析:(1)先求導,再對x分類討論求![]() 的單調性.(2)對a分類討論,求出正實數
的單調性.(2)對a分類討論,求出正實數![]() 的值,使得
的值,使得![]() 為
為![]() 的一個極值.
的一個極值.
詳解:(1)![]() 定義域為
定義域為![]() ,
,![]() .
.
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,故
,故![]() 在
在![]() 單調遞增.
單調遞增.
(2)![]() .
.
因為![]() ,所以當
,所以當![]() 時,
時,![]() .
.
設![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,
,![]() 在
在![]() 單調遞增.
單調遞增.
當![]() 時,
時,![]() ,
,![]() ,
,
故![]() 在
在![]() 有唯一實根
有唯一實根![]()
![]() ,
,![]() .
.
當![]() 時,
時,![]() ,
,![]() ;
;
當![]() 時,
時,![]() ,
,![]() ;
;
當![]() 時,
時,![]() ,
,![]() .
.
所以當![]() 時,
時,![]() 取極小值
取極小值![]() ,
,
當![]() 時,
時,![]() 取極大值
取極大值![]() .
.
令![]() 得
得![]() 不符合
不符合![]() .
.
令![]() ,由①得
,由①得![]() .
.
設![]() ,
,
![]() .
.
當![]() 時
時![]()
故![]() 在
在![]() 單調遞增.因為
單調遞增.因為![]() ,所以
,所以![]() ,
,![]() ,符合
,符合![]() .
.
當![]() 時,由(1)知,沒有極值.
時,由(1)知,沒有極值.
當![]() 時,
時,![]() ,
,![]() ,
,
故![]() 在
在![]() 有唯一實根
有唯一實根![]() ,且
,且![]() .
.
當![]() 時,
時,![]() ,
,![]() ;
;
當![]() 時,
時,![]() ,
,![]() ;
;
當![]() 時
時![]() ,
,![]() .
.
所以當![]() 時,
時,![]() 取極大值
取極大值![]() ,當
,當![]() 時,
時,![]() 取極小值
取極小值![]() .
.
因為![]() ,所以
,所以![]() 不是
不是![]() 的一個極值.
的一個極值.
綜上,存在正實數![]() ,使得
,使得![]() 為
為![]() 的一個極值.
的一個極值.


科目:高中數學 來源: 題型:
【題目】求證:
(1)角![]() 為第二或第三象限角的充要條件是
為第二或第三象限角的充要條件是![]() ;
;
(2)角![]() 為第三或第四象限角的充要條件是
為第三或第四象限角的充要條件是![]() ;
;
(3)角![]() 為第一或第四象限角的充要條件是
為第一或第四象限角的充要條件是![]() ;
;
(4)角![]() 為第一或第三象限角的充要條件是
為第一或第三象限角的充要條件是![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了緩解日益擁堵的交通狀況,不少城市實施車牌競價策略,以控制車輛數量.某地車牌競價的基本規則是:①“盲拍”,即所有參與競拍的人都要網絡報價一次,每個人不知曉其他人的報價,也不知道參與當期競拍的總人數;②競價時間截止后,系統根據當期車牌配額,按照競拍人的出價從高到低分配名額.某人擬參加![]() 年
年![]() 月份的車牌競拍,他為了預測最低成交價,根據競拍網站的數據,統計了最近
月份的車牌競拍,他為了預測最低成交價,根據競拍網站的數據,統計了最近![]() 個月參與競拍的人數(見下表):
個月參與競拍的人數(見下表):
月份 |
|
|
|
|
|
月份編號 |
|
|
|
|
|
競拍人數 |
|
|
|
|
|
(1)由收集數據的散點圖發現,可用線性回歸模型擬合競拍人數![]() (萬人)與月份編號
(萬人)與月份編號![]() 之間的相關關系.請用最小二乘法求
之間的相關關系.請用最小二乘法求![]() 關于
關于![]() 的線性回歸方程:
的線性回歸方程:![]() ,并預測
,并預測![]() 年
年![]() 月份參與競拍的人數.
月份參與競拍的人數.
(2)某市場調研機構從擬參加![]() 年
年![]() 月份車牌競拍人員中,隨機抽取了
月份車牌競拍人員中,隨機抽取了![]() 人,對他們的擬報價價格進行了調查,得到如下頻數分布表和頻率分布直方圖:
人,對他們的擬報價價格進行了調查,得到如下頻數分布表和頻率分布直方圖:
報價區間(萬元) |
|
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
|
(i)求![]() 、
、![]() 的值及這
的值及這![]() 位競拍人員中報價大于
位競拍人員中報價大于![]() 萬元的概率;
萬元的概率;
(ii)若![]() 年
年![]() 月份車牌配額數量為
月份車牌配額數量為![]() ,假設競拍報價在各區間分布是均勻的,請你根據以上抽樣的數據信息,預測(需說明理由)競拍的最低成交價.
,假設競拍報價在各區間分布是均勻的,請你根據以上抽樣的數據信息,預測(需說明理由)競拍的最低成交價.
參考公式及數據:①回歸方程![]() ,其中
,其中 ,
,![]() ;
;
②![]() ,
,![]() .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】20名學生某次數學考試成績(單位:分)的頻率分布直方圖如下:

(1)求頻率直方圖中a的值;
(2)分別求出成績落在[50,60)與[60,70)中的學生人數;
(3)從成績在[50,70)的學生中人選2人,求這2人的成績都在[60,70)中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ln(ax2+x+6).
(1)若a=﹣1,求f(x)的定義域,并討論f(x)的單調性;
(2)若函數f(x)的定義域為R,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】蚌埠市某中學高三年級從甲(文)、乙(理)兩個科組各選出![]() 名學生參加高校自主招生數學選拔考試,他們取得的成績的莖葉圖如圖所示,其中甲組學生的平均分是
名學生參加高校自主招生數學選拔考試,他們取得的成績的莖葉圖如圖所示,其中甲組學生的平均分是![]() ,乙組學生成績的中位數是
,乙組學生成績的中位數是![]() .
.
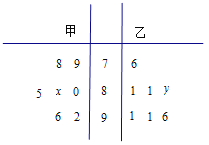
(1)求![]() 和
和![]() 的值;
的值;
(2)計算甲組![]() 位學生成績的方差
位學生成績的方差![]() ;
;
(3)從成績在![]() 分以上的學生中隨機抽取兩名學生,求甲組至少有一名學生的概率.
分以上的學生中隨機抽取兩名學生,求甲組至少有一名學生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拋物線頂點在原點,焦點在x軸上,且過點(4,4),焦點為F.
(1)求拋物線的焦點坐標和標準方程;
(2)P是拋物線上一動點,M是PF的中點,求M的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() ,關于
,關于![]() 的不等式
的不等式![]() 的解集為
的解集為![]() .
.
(Ⅰ)求![]() 、
、![]() 的值;
的值;
(Ⅱ)設![]() .
.
(i)若不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍;
的取值范圍;
(ii)若函數![]() 有三個不同的零點,求實數
有三個不同的零點,求實數![]() 的取值范圍(
的取值范圍(![]() 為自然對數的底數).
為自然對數的底數).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com