解答:
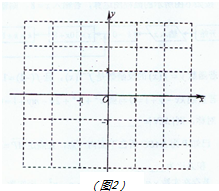
解:(1)在平面直角坐標系中如圖2,
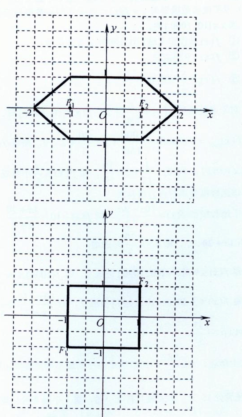
所有滿足到原點的“直角距離”為2的“格點”的坐標有:
(0,2,),(1,1),(2,0),(1,-1),
(0,-2),(-1,-1),(-2,0),(-1,1).
(2)條件①軌跡方程為|x+1|+|x-1|+2|y|=4,
當x≤-1,y≥0時,x-y+2=0;
當x≤-1,y<0時,x+y+2=0;
當-1<x<1,y≥0時,y=1;
當-1<x<1,y<0時,y=-1;
當x≥1,y≥0時,x+y-2=0;
當x≥1,y<0時,x-y-2=0.
條件②軌跡方程為:
|x+1|+|y+1|+|x-1|+|y-1|=4,
當x≤-1,y≥1時,(x,y)=(-1,1);
當x≤-1,-1≤y<1時,x=-1;
當-1<x<1,y≥1時,y=1;
由對稱性可得其他部分圖形.
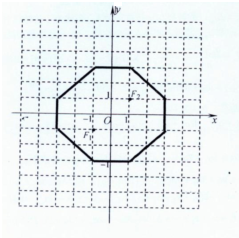
條件③:軌跡方程為:
|x+1|+|y+1|+|x-1|+|y-1|=8,
當x≤-1,y≥1時,x-y+3=0;
當x≤-1,-1≤y<1時,x+3=0;
當-1<x<1,y≥1時,y=3.
由對稱性可得其他部分圖形.
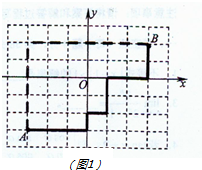
(3)如圖,滿足條件的格點有(-2,2),(-1,2),
(-2,1),(-1,1),(0,0),(1,-1),
(2,-1),(1,-2),(2,-2),
對于①,設P(x,y)滿足到A(-1,-1)、B(1,1)兩點
“直角距離”相等,
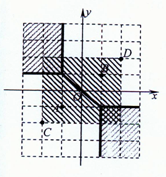
即滿足|x+1|+|y+1|=|x-1|+|y-1|,
解得p∈{(x,y)|x+y=0,-1≤x≤1或x≤-1,y≥1或x≥1,y≤-1},如圖.
對于②,設P(x,y)到C(-2,-2),D(2,2)兩點“直角距離”和最小,
即D
(PA)+D
(PB)=|x+2|+|y+2|+|x-2|+|y-2|
=|x+2|+|x-2|+|y+2|+|y-2|
≥|x+2+2-x|+|y+2+2-y|=8,
當且僅當-2≤x≤2且-2≤y≤2等號成立,
可得點P∈{(x,y)|-2≤x≤2,-2≤y≤2}.如圖
故同時滿足條件①②的格點的坐標是:
(-2,2),(-1,2),(-2,1),(-1,1),(0,0),
(1,-1),(2,-1),(1,-2),(2,-2).






 閱讀快車系列答案
閱讀快車系列答案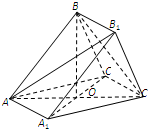 如圖所示,三棱柱ABC-A1B1C1中,AB=AC=AA1=2,平面ABC1⊥平面A1ACC1,
如圖所示,三棱柱ABC-A1B1C1中,AB=AC=AA1=2,平面ABC1⊥平面A1ACC1,