
【題目】已知橢圓![]() 的右頂點、上頂點分別為A、B,坐標原點到直線AB的距離為
的右頂點、上頂點分別為A、B,坐標原點到直線AB的距離為![]() ,且
,且![]() .
.

(1)求橢圓C的方程;
(2)過橢圓C的左焦點![]() 的直線
的直線![]() 交橢圓于M、N兩點,且該橢圓上存在點P,使得四邊形MONP(圖形上字母按此順序排列)恰好為平行四邊形,求直線
交橢圓于M、N兩點,且該橢圓上存在點P,使得四邊形MONP(圖形上字母按此順序排列)恰好為平行四邊形,求直線![]() 的方程.
的方程.
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)是否存在![]() ,
,![]() ,使得函數
,使得函數![]() 在區間
在區間![]() 的最小值為
的最小值為![]() 且最大值為
且最大值為![]() ?若存在,求出
?若存在,求出![]() ,
,![]() 的所有值;若不存在,請說明理由.
的所有值;若不存在,請說明理由.
參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司決定投人資金進行產品研發以提高產品售價.已知每件產品的制造成本為![]() 元,若投人的總的研發成本
元,若投人的總的研發成本![]() (萬元)與每件產品的銷售單價
(萬元)與每件產品的銷售單價![]() (元)的關系如下表:
(元)的關系如下表:
![]()
(1)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)市場部發現,銷售單價![]() (元)與銷量
(元)與銷量![]() (件)存在以下關系:
(件)存在以下關系:![]() ,
,![]() .根據(1)中結果預測,當
.根據(1)中結果預測,當![]() 為何值時,可獲得最高的利潤?
為何值時,可獲得最高的利潤?
附: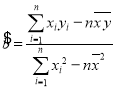 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某城市中心花園的邊界是圓心為O,直徑為1千米的圓,花園一側有一條直線型公路l,花園中間有一條公路AB(AB是圓O的直徑),規劃在公路l上選兩個點P,Q,并修建兩段直線型道路PB,QA.規劃要求:道路PB,QA不穿過花園.已知![]() ,
,![]() (CD為垂足),測得OC=0.9,BD=1.2(單位:千米).已知修建道路費用為m元/千米.在規劃要求下,修建道路總費用的最小值為_____元.
(CD為垂足),測得OC=0.9,BD=1.2(單位:千米).已知修建道路費用為m元/千米.在規劃要求下,修建道路總費用的最小值為_____元.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}為等差數列,a1=1,前n項和為Sn,數列{bn}為等比數列,b1>1,公比為2,且b2S3=54,b3+S2=16.
(Ⅰ)求數列{an}與{bn}的通項公式;
(Ⅱ)設數列{cn}滿足cn=an+bn,求數列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)當a>0時,求函數f(x)的單調區間;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在等比數列{an}中,![]() =2,,
=2,,![]() =128,數列{bn}滿足b1=1,b2=2,且{
=128,數列{bn}滿足b1=1,b2=2,且{![]() }為等差數列.
}為等差數列.
(1)求數列{an}和{bn}的通項公式;
(2)求數列{bn}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產一批零件,為了解這批零件的質量狀況,檢驗員從這批產品中隨機抽取了100件作為樣本進行檢測,將它們的重量(單位:g)作為質量指標值.由檢測結果得到如下頻率分布直方圖.
分組 | 頻數 | 頻率 |
| 8 | |
| ||
| ||
| 16 | 0.16 |
| 4 | 0.04 |
合計 | 100 | 1 |
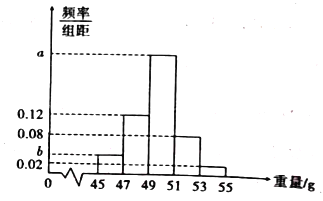
(1)求圖中![]() 的值;
的值;
(2)根據質量標準規定:零件重量小于47或大于53為不合格品,重量在區間![]() 和
和![]() 內為合格品,重量在區間
內為合格品,重量在區間![]() 內為優質品.已知每件產品的檢測費用為5元,每件不合格品的回收處理費用為20元.以抽檢樣本重量的頻率分布作為該零件重量的概率分布.若這批零件共
內為優質品.已知每件產品的檢測費用為5元,每件不合格品的回收處理費用為20元.以抽檢樣本重量的頻率分布作為該零件重量的概率分布.若這批零件共![]() 件
件![]() ,現有兩種銷售方案:方案一:不再檢測其他零件,整批零件除對已檢測到的不合格品進行回收處理,其余零件均按150元/件售出;方案二:繼續對剩余零件的重量進行逐一檢測,回收處理所有不合格品,合格品按150元/件售出,優質品按200元/件售出.僅從獲得利潤大的角度考慮,該生產商應選擇哪種方案?請說明理由.
,現有兩種銷售方案:方案一:不再檢測其他零件,整批零件除對已檢測到的不合格品進行回收處理,其余零件均按150元/件售出;方案二:繼續對剩余零件的重量進行逐一檢測,回收處理所有不合格品,合格品按150元/件售出,優質品按200元/件售出.僅從獲得利潤大的角度考慮,該生產商應選擇哪種方案?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知![]() 是橢圓
是橢圓![]() 的左焦點,且橢圓
的左焦點,且橢圓![]() 經過點
經過點![]() .
.
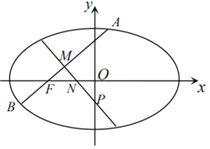
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,過
,過![]() 且與
且與![]() 垂直的直線與
垂直的直線與![]() 軸和
軸和![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,記
兩點,記![]() 、
、![]() 的面積分別為
的面積分別為![]() 、
、![]() .若
.若![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com