
 ,
, .
. 為
為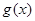 的導(dǎo)函數(shù),若不等式
的導(dǎo)函數(shù),若不等式 在
在 上有解,求實(shí)數(shù)
上有解,求實(shí)數(shù)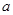 的取值范圍;
的取值范圍; ,對(duì)任意的
,對(duì)任意的 ,不等式
,不等式 恒成立,求m(m∈Z,m
恒成立,求m(m∈Z,m 1)的值.
1)的值.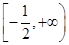 ;(2)
;(2)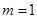 .
.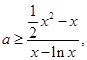 它在
它在 上有解等價(jià)于
上有解等價(jià)于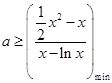 ,再利用導(dǎo)數(shù)求函數(shù)
,再利用導(dǎo)數(shù)求函數(shù) 的最小值;(2)由已知
的最小值;(2)由已知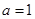 時(shí),對(duì)任意的
時(shí),對(duì)任意的 ,不等式
,不等式 恒成立,等價(jià)變形為
恒成立,等價(jià)變形為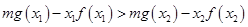 在
在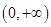 上恒成立,為此只需構(gòu)造函數(shù)
上恒成立,為此只需構(gòu)造函數(shù)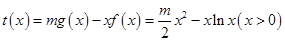 ,只要證明函數(shù)
,只要證明函數(shù)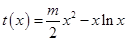 在
在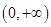 上單調(diào)遞增即可.
上單調(diào)遞增即可.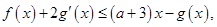 即為
即為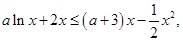 化簡(jiǎn)得
化簡(jiǎn)得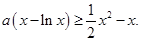 由
由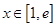 知
知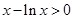 ,因而
,因而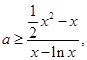 設(shè)
設(shè) 由
由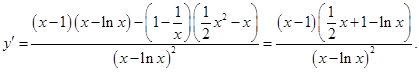
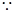 當(dāng)
當(dāng)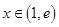 時(shí)
時(shí)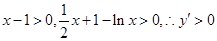 在
在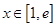 上恒成立.
上恒成立.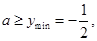 即實(shí)數(shù)
即實(shí)數(shù)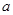 的取值范圍是
的取值范圍是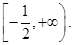
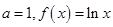 .由
.由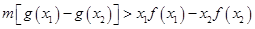 恒成立,得
恒成立,得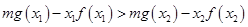 恒成立. 設(shè)
恒成立. 設(shè)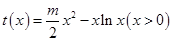 ,
, ,故當(dāng)
,故當(dāng)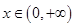 時(shí)函數(shù)
時(shí)函數(shù)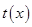 單調(diào)遞增,
單調(diào)遞增,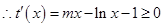 恒成立,即
恒成立,即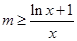 恒成立,因此,記
恒成立,因此,記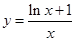 ,得
,得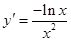 ,
,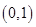 上單調(diào)遞增,在
上單調(diào)遞增,在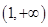 上單調(diào)遞減,∴函數(shù)
上單調(diào)遞減,∴函數(shù)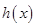 在
在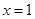 時(shí)取得極大值,并且這個(gè)極大值就是函數(shù)
時(shí)取得極大值,并且這個(gè)極大值就是函數(shù)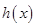 的最大值.由此可得
的最大值.由此可得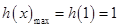 ,故
,故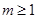 ,結(jié)合已知條件
,結(jié)合已知條件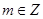 ,
,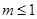 ,可得
,可得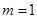 .
.


| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:解答題
 的圓形(
的圓形( 為圓心)鐵皮上截取一塊矩形材料
為圓心)鐵皮上截取一塊矩形材料 ,其中點(diǎn)
,其中點(diǎn) 在圓弧上,點(diǎn)
在圓弧上,點(diǎn) 在兩半徑上,現(xiàn)將此矩形材料卷成一個(gè)以
在兩半徑上,現(xiàn)將此矩形材料卷成一個(gè)以 為母線的圓柱形罐子的側(cè)面(不計(jì)剪裁和拼接損耗),設(shè)
為母線的圓柱形罐子的側(cè)面(不計(jì)剪裁和拼接損耗),設(shè) 與矩形材料的邊
與矩形材料的邊 的夾角為
的夾角為 ,圓柱的體積為
,圓柱的體積為
 .
.
 關(guān)于
關(guān)于 的函數(shù)關(guān)系式?
的函數(shù)關(guān)系式? 的最大值.
的最大值.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:解答題
 (
( ).
). 時(shí),求函數(shù)
時(shí),求函數(shù) 的極值;
的極值;  ,不等式
,不等式 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù) 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:單選題
 ,則
,則 是函數(shù)
是函數(shù)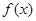 的極值點(diǎn),因?yàn)楹瘮?shù)
的極值點(diǎn),因?yàn)楹瘮?shù) 在
在 處的導(dǎo)數(shù)值
處的導(dǎo)數(shù)值 ,所以
,所以 是函數(shù)
是函數(shù) 的極值點(diǎn).你認(rèn)為以上推理的 ( )
的極值點(diǎn).你認(rèn)為以上推理的 ( )| A.大前提錯(cuò)誤 | B.小前提錯(cuò)誤 | C.推理形式錯(cuò)誤 | D.結(jié)論正確 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:解答題
 在
在 時(shí)有極大值6,在
時(shí)有極大值6,在 時(shí)有極小值
時(shí)有極小值 的值;并求
的值;并求 在區(qū)間[-3,3]上的最大值和最小值.
在區(qū)間[-3,3]上的最大值和最小值.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com