Question

4．設函數f（x）=|x-a|+|2x+2|-5（a∈R）．
（Ⅰ）試比較f（-1）與f（a）的大小；
（Ⅱ）當a=-5時，求函數f（x）的圖象與軸圍成的圖形面積．

Answer 1

分析 （Ⅰ）f（-1）與f（a）作差化簡表達式推出結果．
（Ⅱ）去掉絕對值，通過三角形的坐標，推出面積，得到結果．

解答 解：（I）因為f（a）-f（-1）=|2a+2|-5-（|a+1|-5）=|a+1|≥0，于是f（a）≥f（-1）．
當且僅當a=-1時等號成立；…5分
（Ⅱ）當a=-5時，$f（x）=|{x+5}|+|{2x+2}|-5=\left\{\begin{array}{l}3x+2，x≥-1\\-x-2，-5≤x＜-1\\-3x-12，x＜-5\end{array}\right.$，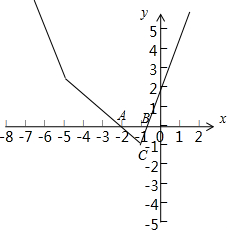
可知函數f（x）的圖象和軸圍成的圖形是一個三角形，
其中與軸的兩個交點分別為A（-2，0），$B（-\frac{2}{3}，0）$，
三角形另一頂點坐標為C（-1，-1），
從而△ABC面積為$S=\frac{1}{2}×（2-\frac{2}{3}）×1=\frac{2}{3}$．…10分
注：以上各題，其他解法請酌情給分．

點評 本題考查含絕對值代數式大小比較，絕對值函數圖象特征等基礎知識，以及分類討論思想和運算求解能力，中等題．