
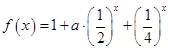 ;
;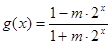 .
.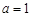 時,求函數(shù)f(x)在
時,求函數(shù)f(x)在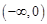 上的值域;
上的值域;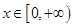 ,總有
,總有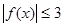 成立,求實數(shù)
成立,求實數(shù)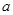 的取值范圍;
的取值范圍;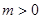 (
(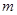 為常數(shù)),且對任意
為常數(shù)),且對任意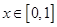 ,總有
,總有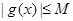 成立,求M的取值范圍.
成立,求M的取值范圍.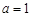 時,
時,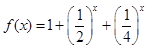 因為f(x)在
因為f(x)在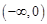 上遞減,…………2分
上遞減,…………2分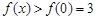 ,即f(x)在
,即f(x)在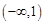 的值域為
的值域為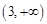 …………4分
…………4分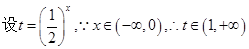 ,
,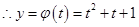 ,對稱軸
,對稱軸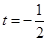 ,
,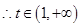 時為增函數(shù),…………2分
時為增函數(shù),…………2分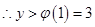 ,f(x)在
,f(x)在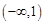 的值域為
的值域為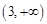 …………4分
…………4分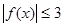 在
在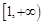 上恒成立。
上恒成立。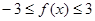 ,
, 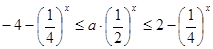 ∴
∴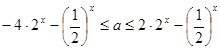 在
在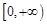 上恒成立,
上恒成立,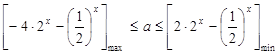 …………6分
…………6分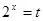 ,
,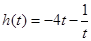 ,
,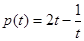 ,由
,由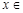
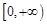 得 t≥1,
得 t≥1,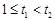 ,,
,,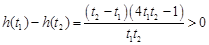
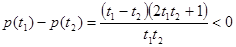
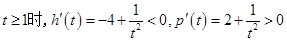 )
)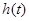 在
在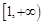 上遞減,
上遞減, 在
在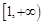 上遞增,…………8分
上遞增,…………8分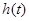 在
在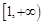 上的最大值為
上的最大值為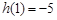 ,
, 在
在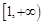 上的最小值為
上的最小值為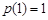
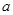 的取值范圍為
的取值范圍為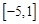 …………10分
…………10分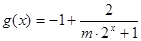 ,∵ m>0 ,
,∵ m>0 ,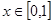 ∴
∴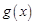 在
在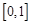 上遞減,
上遞減,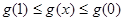 即
即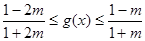 …………11分
…………11分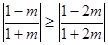 ,即
,即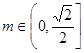 時,
時,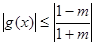 ,此時
,此時 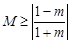 ,…………12分
,…………12分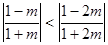 ,即
,即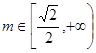 時,
時,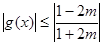 ,
,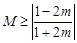 ,…………13分
,…………13分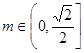 時,M的取值范圍是
時,M的取值范圍是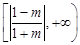 ;
;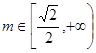 時,M的取值范圍是
時,M的取值范圍是 …………14分
…………14分

科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
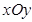 中,過坐標(biāo)原點
中,過坐標(biāo)原點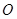 的一條直線
的一條直線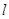 與函數(shù)
與函數(shù)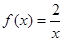 的圖象交于P、Q兩點,則線段PQ長的最小值是________.此時,由直線
的圖象交于P、Q兩點,則線段PQ長的最小值是________.此時,由直線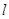 、函數(shù)
、函數(shù)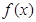 及直線x=4圍成封閉圖形的面積是______________
及直線x=4圍成封閉圖形的面積是______________查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
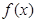 的定義域關(guān)于原點對稱,但不包括數(shù)0,對定義域中的任意實數(shù)
的定義域關(guān)于原點對稱,但不包括數(shù)0,對定義域中的任意實數(shù)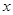 ,在定義域中存在
,在定義域中存在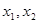 使
使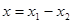 ,
,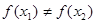 ,且滿足以下3個條件。
,且滿足以下3個條件。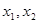 是
是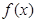 定義域中的數(shù),
定義域中的數(shù),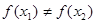 ,則
,則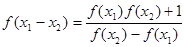
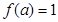 ,(
,(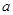 是一個正的常數(shù))
是一個正的常數(shù))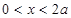 時,
時,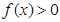 。
。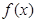 是奇函數(shù);
是奇函數(shù);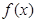 是周期函數(shù),并求出其周期;
是周期函數(shù),并求出其周期;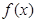 在
在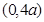 內(nèi)為減函數(shù)。
內(nèi)為減函數(shù)。查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
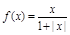 (x
(x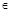 R),四位同學(xué)甲、乙、丙、丁在研究此函數(shù)時分別給出命題:甲:函數(shù)f(x)的值域為(-1,1);乙:若x1≠x2,則一定有f(x1)≠f(x2);丙:若規(guī)定
R),四位同學(xué)甲、乙、丙、丁在研究此函數(shù)時分別給出命題:甲:函數(shù)f(x)的值域為(-1,1);乙:若x1≠x2,則一定有f(x1)≠f(x2);丙:若規(guī)定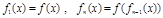 ,
,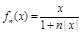 對任意
對任意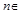 N*恒成立;丁:函數(shù)
N*恒成立;丁:函數(shù)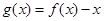 在
在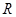 上有三個零點。上述四個命題中你認(rèn)為正確的是_____________(用甲、乙、丙、丁作答)。
上有三個零點。上述四個命題中你認(rèn)為正確的是_____________(用甲、乙、丙、丁作答)。查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com