
分析 (1)將(1,1)帶入,找到a,b的等式關(guān)系.利用基本不等式的可得答案.
(2)函數(shù)y定義域?yàn)镽,只需(m2-3m+2)x2+2(m-1)x+5≥0,即△≤0,m2-3m+2>0可得實(shí)數(shù)m的取值范圍
解答 解:(1)直線$\frac{x}{a}+\frac{y}{b}$=1(a>0,b>0),過點(diǎn)(1,1),
可得$\frac{1}{a}+\frac{1}{b}=1$,
那么:a+b=(a+b)($\frac{1}{a}+\frac{1}{b}$)=2+$\frac{a}{b}+\frac{b}{a}$≥2$+2\sqrt{\frac{a}{b}×\frac{b}{a}}=4$(當(dāng)且僅當(dāng)a=b時(shí)取等號)
故得a+b的最小值為4.
(2)由題意,函數(shù)y定義域?yàn)镽,只需(m2-3m+2)x2+2(m-1)x+5≥0,即△≤0,m2-3m+2>0,
則4(m-1)2-20(m2-3m+2)≤0,且m2-3m+2>0,
解得:$m≥\frac{9}{4}$或m≤1,且m>2或m<1.
當(dāng)m2-3m+2=0時(shí),可得m=1或m=2,若m=1,則方程恒為正.
故得實(shí)數(shù)m的取值范圍是$(-∞,1]∪[\frac{9}{4},+∞)$.
點(diǎn)評 本題考查了基本不等式的性質(zhì)的運(yùn)用和二次不等式的解法和性質(zhì).屬于基礎(chǔ)題.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
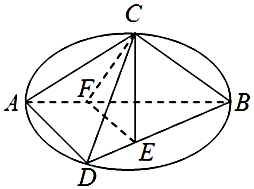 如圖C,D是以AB為直徑的圓上的兩點(diǎn),AB=2AD=2$\sqrt{3}$,AC=BC,F(xiàn)是AB上的一點(diǎn),且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.
如圖C,D是以AB為直徑的圓上的兩點(diǎn),AB=2AD=2$\sqrt{3}$,AC=BC,F(xiàn)是AB上的一點(diǎn),且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | e+1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
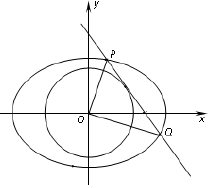 如圖,已知橢圓C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{{\sqrt{2}}}{2}$,點(diǎn)(2,1)在橢圓C上.
如圖,已知橢圓C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{{\sqrt{2}}}{2}$,點(diǎn)(2,1)在橢圓C上.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $-\frac{9}{4}$ | B. | $\frac{9}{4}$ | C. | $\frac{27}{4}$ | D. | $-\frac{27}{4}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | y=2-|x| | B. | y=tanx | C. | y=-x3 | D. | $y={log_{\frac{1}{5}}}x$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
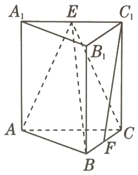 如圖,在三棱柱ABC-A1B1C1中,側(cè)棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F(xiàn)分別為A1C1,BC的中點(diǎn).
如圖,在三棱柱ABC-A1B1C1中,側(cè)棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F(xiàn)分別為A1C1,BC的中點(diǎn).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com