
【題目】已知函數![]() 為
為![]() 上的偶函數,
上的偶函數, ![]() 為
為![]() 上的奇函數,且
上的奇函數,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若函數![]() 在
在![]() 上只有一個零點,求實數
上只有一個零點,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)詳見解析;(2) ![]() 或
或![]() .
.
【解析】試題分析:本題根據函數的奇偶性,采用方程組法求函數的解析式,把已知條件里的x替換為-x,利用函數的奇偶性,得出一個新的關系式,兩式聯立,解出函數f(x)和g(x)的解析式,寫出函數h(x),令h(x)=0,轉化為方程只有一根,利用換元法轉化為二次方程只有一個正根,包括一個正根一個負根及兩個相等正根兩種情況,分別按要求解出a的范圍.
試題解析:
(1)![]() ①
①
![]() .
.
![]() ②
②
由①②得:
![]() ,
, ![]()
由(1)可得:
![]()
![]()
![]() 在
在![]() 上只有一個零點
上只有一個零點
![]() 只有一個實數根
只有一個實數根
即![]() 只有一個實數根
只有一個實數根
令![]()
則![]()
![]() 只有一個正實數根
只有一個正實數根
①當![]() 時,
時, ![]() 符合題意
符合題意
②當![]() 時,令
時,令![]()
若![]() 有一正一負實數根,則
有一正一負實數根,則![]() 或
或![]() ,解得
,解得![]() ;
;
若![]() 有兩個相等的正實數根,則
有兩個相等的正實數根,則![]() ,解得
,解得![]() 或
或![]() (舍)
(舍)
![]() 時,
時, ![]() 。
。
綜上所述: ![]() 得取值范圍是
得取值范圍是![]() 或
或![]() .
.
【點精】關于求函數的解析式問題常用方法有待定系數法、換元法、方程組法等,本題采用的方法為方程組法;當已知函數為哪種基本初等函數時,按照函數的定義形式設出函數,利用待定系數法求出解析式;當提供復合函數形式時,利用換元法求出解析式,但要注意函數的定義域;方程組法題型較少,易于掌握,函數零點問題有時化成函數圖象與x軸的交點問題,有時化為方程的根的的問題,有時化為兩個函數圖象的交點問題,有時還需借助導數研究函數圖象去解決.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,某村積極開展“美麗鄉村生態家園”建設,現擬在邊長為1千米的正方形地塊ABCD上劃出一片三角形地塊CMN建設美麗鄉村生態公園,給村民休閑健身提供去處.點M,N分別在邊AB,AD上. (Ⅰ)當點M,N分別是邊AB,AD的中點時,求∠MCN的余弦值;
(Ⅱ)由于村建規劃及保護生態環境的需要,要求△AMN的周長為2千米,請探究∠MCN是否為定值,若是,求出此定值,若不是,請說明理由.
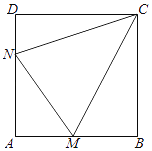
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (a>0,a≠1,m≠﹣1),是定義在(﹣1,1)上的奇函數.
(a>0,a≠1,m≠﹣1),是定義在(﹣1,1)上的奇函數.
(I)求f(0)的值和實數m的值;
(II)當m=1時,判斷函數f(x)在(﹣1,1)上的單調性,并給出證明;
(III)若![]() 且f(b﹣2)+f(2b﹣2)>0,求實數b的取值范圍.
且f(b﹣2)+f(2b﹣2)>0,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的正方形中隨機投擲10 000個點,則落入陰影部分(曲線C為正態分布
N(-1,1)的部分密度曲線)的點的個數的估計值為
附:若X~N(μ,σ2),則P(μ-σ<X<μ+σ)=0.682 6,P(μ-2σ<X<μ+2σ)=0.954 4.
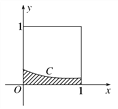
A. 1 193 B. 1 359 C. 2 718 D. 3 413
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們可以用隨機模擬的方法估計![]() 的值,如圖程序框圖表示其基本步驟(函數
的值,如圖程序框圖表示其基本步驟(函數![]() 是產生隨機數的函數,它能隨機產生
是產生隨機數的函數,它能隨機產生![]() 內的任何一個實數).若輸出的結果為
內的任何一個實數).若輸出的結果為![]() ,則由此可估計
,則由此可估計![]() 的近似值為( )
的近似值為( )
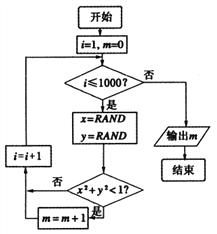
A. 3.119 B. 3.124 C. 3.132 D. 3.151
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知奇函數![]() 在區間
在區間![]() 上是增函數,且最大值為10,最小值為4,則在區間
上是增函數,且最大值為10,最小值為4,則在區間![]() 上
上![]() 的最大值、最小值分別是( )
的最大值、最小值分別是( )
A. -4,-10 B. 4,-10
C. 10,4 D. 不確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校高三年級有學生1 000名,經調查,其中750名同學經常參加體育鍛煉(稱為A類同學),另外250名同學不經常參加體育鍛煉(稱為B類同學),現用分層抽樣方法(按A類、B類分兩層)從該年級的學生中共抽查100名同學,如果以身高達165 cm作為達標的標準,對抽取的100名學生,得到以下列聯表:
身高達標 | 身高不達標 | 總計 | |
經常參加體育鍛煉 | 40 | ||
不經常參加體育鍛煉 | 15 | ||
總計 | 100 |
(1)完成上表;
(2)能否在犯錯誤的概率不超過0.05的前提下認為經常參加體育鍛煉與身高達標有關系(K2的觀測值精確到0.001)?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com