
【題目】已知函數f(x)= ![]()
(1)求證f(x)在(0,+∞)上遞增
(2)若f(x)在[m,n]上的值域是[m,n],求實數a的取值范圍
(3)當f(x)≤2x在(0,+∞)上恒成立,求實數a的取值范圍.
【答案】
(1)證明:∵f(x)= ![]() ﹣
﹣ ![]() ,x∈(0,+∞),
,x∈(0,+∞),
∴f'(x)= ![]() >0,
>0,
故函數f(x)在(0,+∞)上單調遞增
(2)∵f(x)在(0,+∞)上單調遞增,
∴若f(x)在[m,n]上的值域是[m,n],
則 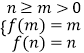 ,即
,即 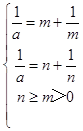 ,
,
故函數y= ![]() 與y=x+
與y=x+ ![]() (x>0)的圖象有兩個公共點,
(x>0)的圖象有兩個公共點,
∵當x>0時,y=x+ ![]() ≥2(當且僅當x=
≥2(當且僅當x= ![]() ,即x=1時取“=”),
,即x=1時取“=”),
∴ ![]() ≥2,解得0<a≤
≥2,解得0<a≤ ![]()
(3)∵f(x)= ![]() ﹣
﹣ ![]() ,f(x)≤2x在(0,+∞)上恒成立上,
,f(x)≤2x在(0,+∞)上恒成立上,
∴a≥ ![]() =
= ![]() 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
令g(x)= ![]() ,
,
則g(x)≤ ![]() =
= ![]() (當且僅當2x=
(當且僅當2x= ![]() ,即x=
,即x= ![]() 時取等號),
時取等號),
要使(0,+∞)上恒成立,
故a的取值范圍是[ ![]() ,+∞)
,+∞)
【解析】(1)利用f'(x)= ![]() >0即可證明f(x)在(0,+∞)上遞增;(2)若f(x)在[m,n]上的值域是[m,n],則則
>0即可證明f(x)在(0,+∞)上遞增;(2)若f(x)在[m,n]上的值域是[m,n],則則 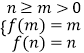 ,構造函數y=
,構造函數y= ![]() 與y=x+
與y=x+ ![]() (x>0),利用兩函數的圖象有兩個公共點,即求實數a的取值范圍;(3)當f(x)≤2x在(0,+∞)上恒成立a≥
(x>0),利用兩函數的圖象有兩個公共點,即求實數a的取值范圍;(3)當f(x)≤2x在(0,+∞)上恒成立a≥ ![]() =
= ![]() 在(0,+∞)上恒成立,構造函數g(x)=
在(0,+∞)上恒成立,構造函數g(x)= ![]() ,利用基本不等式可求得g(x)max , 從而可求實數a的取值范圍.
,利用基本不等式可求得g(x)max , 從而可求實數a的取值范圍.
【考點精析】利用函數的值域對題目進行判斷即可得到答案,需要熟知求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線y2=4x的焦點為F,過點F的直線交拋物線于A,B兩點.
(1)若 ![]() =3
=3 ![]() ,求直線AB的斜率;
,求直線AB的斜率;
(2)設點M在線段AB上運動,原點O關于點M的對稱點為C,求四邊形OACB面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】山西某公司有一批專業技術人員,對他們進行年齡狀況和接受教育程度(本科學歷)的調查,其結果(人數分布)如表:
學歷 | 35歲以下 | 35 | 50歲以上 |
本科 | 80 | 30 | 20 |
研究生 |
| 20 |
|
(Ⅰ)用分層抽樣的方法在![]() 歲年齡段的專業技術人員中抽取一個容量為10的樣本,將該樣本看成一個總體,從中任取3人,求至少有1人的學歷為研究生的概率;
歲年齡段的專業技術人員中抽取一個容量為10的樣本,將該樣本看成一個總體,從中任取3人,求至少有1人的學歷為研究生的概率;
(Ⅱ)在這個公司的專業技術人員中按年齡狀況用分層抽樣的方法抽取![]() 個人,其中35歲以下48人,50歲以上10人,再從這
個人,其中35歲以下48人,50歲以上10人,再從這![]() 個人中隨機抽取出1人,此人的年齡為50歲以上的概率為
個人中隨機抽取出1人,此人的年齡為50歲以上的概率為![]() ,求
,求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設x取實數,則f(x)與g(x)表示同一個函數的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)= ![]() ,g(x)=
,g(x)= ![]()
C.f(x)=1,g(x)=(x﹣1)0
D.f(x)= ![]() ,g(x)=x﹣3
,g(x)=x﹣3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017北京西城區5月模擬】某大學為調研學生在![]() ,
,![]() 兩家餐廳用餐的滿意度,從在
兩家餐廳用餐的滿意度,從在![]() ,
,![]() 兩家餐廳都用過餐的學生中隨機抽取了100人,每人分別對這兩家餐廳進行評分,滿分均為60分.
兩家餐廳都用過餐的學生中隨機抽取了100人,每人分別對這兩家餐廳進行評分,滿分均為60分.
整理評分數據,將分數以10為組距分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到
,得到![]() 餐廳分數的頻率分布直方圖,和
餐廳分數的頻率分布直方圖,和![]() 餐廳分數的頻數分布表:
餐廳分數的頻數分布表:
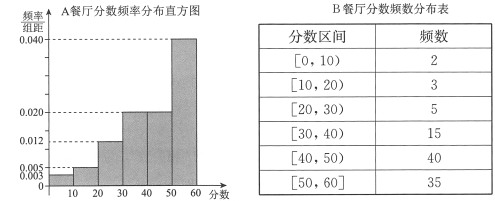
定義學生對餐廳評價的“滿意度指數”如下:
分數 |
|
|
|
滿意度指數 |
|
|
|
(Ⅰ)在抽樣的100人中,求對![]() 餐廳評價“滿意度指數”為0的人數;
餐廳評價“滿意度指數”為0的人數;
(Ⅱ)從該校在![]() ,
,![]() 兩家餐廳都用過餐的學生中隨機抽取1人進行調查,試估計其對
兩家餐廳都用過餐的學生中隨機抽取1人進行調查,試估計其對![]() 餐廳評價的“滿意度指數”比對
餐廳評價的“滿意度指數”比對![]() 餐廳評價的“滿意度指數”高的概率;
餐廳評價的“滿意度指數”高的概率;
(Ⅲ)如果從![]() ,
,![]() 兩家餐廳中選擇一家用餐,你會選擇哪一家?說明理由.
兩家餐廳中選擇一家用餐,你會選擇哪一家?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com