
分析 (1)根據已知得到關于d 的方程解出公差;
(2)利用數列通項與前n項和的關系得到數列{cn}的通項公式,然后求和.
解答 解(1)由已知有a2=1+d,a5=1+4d,a14=1+13d,∴(1+4d)2=(1+d)(1+13d),解得d=2(d=0舍).
∴an=2n-1,又b2=a2=3,b3=a3=9,∴數列{bn}的公比為3,∴bn=3n-1;
(2)由{cn}對n∈N*均有$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{{b}_{2}}$+…+$\frac{{c}_{n}}{{b}_{n}}$=an+1成立得當n≥2時,{cn}對n∈N*均有$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{{b}_{2}}$+…+$\frac{{c}_{n-1}}{{b}_{n-1}}$=an成立,
兩式相減得:當n≥2時,$\frac{{c}_{n}}{{b}_{n}}$=an+1-an=2.
∴cn=2bn=2•3n-1(n≥2).
又當n=1時,$\frac{{c}_{1}}{{b}_{1}}$=a2,∴c1=3,
∴cn=$\left\{\begin{array}{l}{3,n=1}\\{2×{3}^{n-1},n≥2}\end{array}\right.$,
∴c1+c2+c3+…+c2016
=3+(-3+32016)=32016
點評 本題考查了等差數列與等比數列的通項公式的求法以及數列求和;本題注意數列{cn}的通項公式的表示;屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
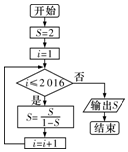
| A. | -$\frac{2}{4029}$ | B. | -$\frac{2}{4030}$ | C. | -$\frac{2}{4031}$ | D. | -$\frac{2}{4033}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com