
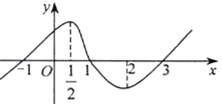
 已知函數y=f(x)(x∈R)的圖象如圖所示,f′(x)是f(x)的導函數,則不等式(x-1)f′(x)<0的解集為(-∞,$\frac{1}{2}$)∪(1,2).
已知函數y=f(x)(x∈R)的圖象如圖所示,f′(x)是f(x)的導函數,則不等式(x-1)f′(x)<0的解集為(-∞,$\frac{1}{2}$)∪(1,2). 分析 通過討論x的符號,根據函數單調性和導數之間的關系即可得到結論.
解答 解:若x-1=0即x=1時,不等式(x-1)•f′(x)<0不成立.
若x-1>0即x>1時,則不等式(x-1)•f′(x)<0等價為f′(x)<0,
此時函數單調遞減,由圖象可知,此時1<x<2.
若x-1<0即x<1時,則不等式(x-1)•f′(x)<0等價為f′(x)>0,
此時函數單調遞增,由圖象可知,此時x<$\frac{1}{2}$.,
故不等式x•f′(x)<0的解集為(-∞,$\frac{1}{2}$)∪(1,2).
故答案為:(-∞,$\frac{1}{2}$)∪(1,2).
點評 本題主要考查不等式的解法,利用函數單調性和導數之間的關系即可得到結論.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|1≤x<2} | B. | {x|x>2} | C. | {x|x≥1或x<0} | D. | {x|x>0} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
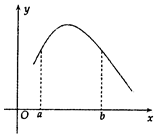 函數f(x)的圖象如圖所示,設f'(x)是f(x)的導函數,若0<a<b,下列各式成立的是( )
函數f(x)的圖象如圖所示,設f'(x)是f(x)的導函數,若0<a<b,下列各式成立的是( )| A. | $f'({\frac{2ab}{a+b}})<f'({\frac{a+b}{2}})<f'({\sqrt{ab}})$ | B. | $f'({\frac{2ab}{a+b}})<f'({\sqrt{ab}})<f'({\frac{a+b}{2}})$ | ||
| C. | $f'({\frac{a+b}{2}})<f'({\frac{2ab}{a+b}})<f'({\sqrt{ab}})$ | D. | $f'({\frac{a+b}{2}})<f'({\sqrt{ab}})<f'({\frac{2ab}{a+b}})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com