Question

5．甲和乙兩人約定在某天早上6：30到7：30之間在校門口見面，假設每人都是隨機的在這個小時內的任意時刻到達，且只等15分鐘．則他們能碰面的概率是$\frac{7}{16}$．

Answer 1

分析 由題意知本題是一個幾何概型，試驗包含的所有事件是Ω={（x，y）|6.5≤x≤7.5，6.5≤y≤7.5}，做出事件對應的集合表示的面積，寫出滿足條件的事件是A={（x，y）|6.5≤x≤7.5，6.5≤y≤7.5，|x-y|≤$\frac{1}{4}$}，算出事件對應的集合表示的面積，根據幾何概型概率公式得到結果．

解答 解：由題意知本題是一個幾何概型，設事件A為“兩人能會面”，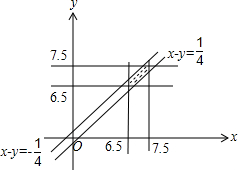
試驗包含的所有事件是Ω={（x，y）|6.5≤x≤7.5，6.5≤y≤7.5}，并且事件對應的集合表示的面積是s=1，
滿足條件的事件是A={（x，y）|6.5≤x≤7.5，6.5≤y≤7.5，|x-y|≤$\frac{1}{4}$}，
∴事件對應的集合表示的面積是1-2×$\frac{1}{2}×\frac{3}{4}×\frac{3}{4}$=$\frac{7}{16}$．
根據幾何概型概率公式得到P=$\frac{7}{16}$．
故答案為：$\frac{7}{16}$．

點評 本題是一個幾何概型，對于這樣的問題，一般要通過把試驗發生包含的事件同集合結合起來，根據集合對應的圖形做出面積，用面積的比值得到結果，是基礎題．