
設函數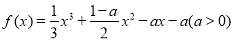 .
.
(1)若函數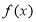 在區間(-2,0)內恰有兩個零點,求a的取值范圍;
在區間(-2,0)內恰有兩個零點,求a的取值范圍;
(2)當a=1時,求函數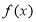 在區間[t,t+3]上的最大值.
在區間[t,t+3]上的最大值.
(1) (2)
(2) 
【解析】
試題分析:
(1)根據題意對函數 求導,獲得導函數
求導,獲得導函數 的根與大于0小于0的解集,獲得函數
的根與大于0小于0的解集,獲得函數 的單調區間和極值點,極值.進而確定函數
的單調區間和極值點,極值.進而確定函數 在區間
在區間 上的單調性,再利用數形結合的思想與零點存在性定理的知識可以得到函數在
上的單調性,再利用數形結合的思想與零點存在性定理的知識可以得到函數在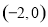 上要有兩個零點,需要
上要有兩個零點,需要 滿足
滿足 即可,解不等式即可求出
即可,解不等式即可求出 的取值范圍.
的取值范圍.
(2)根據題意 ,則利用(1)可以得到
,則利用(1)可以得到 的單調性以及極值點,極值.要得到函數
的單調性以及極值點,極值.要得到函數 在含參數的區間
在含參數的區間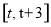 上的最大值,我們需要討論
上的最大值,我們需要討論 的范圍得到函數
的范圍得到函數 的在區間
的在區間 上的單調性進而得到
上的單調性進而得到 在該區間上的最大值,為此分三種情況分別為
在該區間上的最大值,為此分三種情況分別為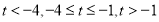 ,依次確定單調性得到最大值即可.
,依次確定單調性得到最大值即可.
試題解析:
(1)∵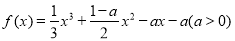
∴ , (1分)
, (1分)
令 ,解得
,解得 (2分)
(2分)
當x變化時, ,
, 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
|
| 0 | — | 0 |
|
| ↗ | 極大值 | ↘ | 極小值 | ↗ |
故函數 的單調遞增區間為(-∞,-1),(a,+∞);單調遞減區間為(-1,a);(4分)
的單調遞增區間為(-∞,-1),(a,+∞);單調遞減區間為(-1,a);(4分)
因此 在區間(-2,-1)內單調遞增,在區間(-1,0)內單調遞減,要使函數
在區間(-2,-1)內單調遞增,在區間(-1,0)內單調遞減,要使函數 在區間
在區間 內恰有兩個零點,當且僅當
內恰有兩個零點,當且僅當 , (5分)
, (5分)
解得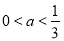 , 所以a的取值范圍是(0,
, 所以a的取值范圍是(0,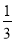 ). (6分)
). (6分)
(2)當a=1時, . 由(1)可知,函數
. 由(1)可知,函數 的單調遞增區間為(-∞,-1),(1,+∞);單調遞減區間為(-1,1);
的單調遞增區間為(-∞,-1),(1,+∞);單調遞減區間為(-1,1); . (7分)
. (7分)
①當t+3<-1,即t<-4時,
因為 在區間[t,t+3]上單調遞增,所以
在區間[t,t+3]上單調遞增,所以 在區間[t,t+3]上的最大值為
在區間[t,t+3]上的最大值為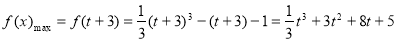 ; (9分)
; (9分)
②當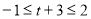 ,即
,即 時,
時,
因為 在區間
在區間 上單調遞增,在區間[-1,1]上單調遞減,在區間[1,2]上單調遞增,且
上單調遞增,在區間[-1,1]上單調遞減,在區間[1,2]上單調遞增,且 ,所以
,所以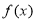 在區間
在區間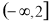 上的最大值為
上的最大值為 . (10分)
. (10分)
由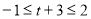 ,即
,即 時,有[t,t+3]?
時,有[t,t+3]? 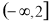 ,-1?[t,t+3],所以
,-1?[t,t+3],所以 在
在 上的最大值為
上的最大值為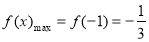 ; (11分)
; (11分)
③當t+3>2,即t>-1時,
由②得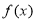 在區間
在區間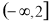 上的最大值為
上的最大值為 .
.
因為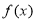 在區間(1,+∞)上單調遞增,所以
在區間(1,+∞)上單調遞增,所以 ,
,
故 在
在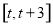 上的最大值為
上的最大值為 . (13分)
. (13分)
綜上所述,當a=1時,
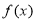 在[t,t+3]上的最大值
在[t,t+3]上的最大值 . (14分)
. (14分)
考點:導數 最值 零點


 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:高中數學 來源:2013-2014學年廣東省韶關市高三4月高考模擬(二模)理科數學試卷(解析版) 題型:選擇題
若直角坐標平面內的兩不同點 、
、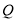 滿足條件:①
滿足條件:① 、
、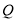 都在函數
都在函數 的圖像上;②
的圖像上;② 、
、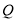 關于原點對稱,則稱點對
關于原點對稱,則稱點對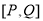 是函數
是函數 的一對“友好點對”(注:點對
的一對“友好點對”(注:點對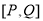 與
與 看作同一對“友好點對”).已知函數
看作同一對“友好點對”).已知函數 =
= ,則此函數的“友好點對”有( )對.
,則此函數的“友好點對”有( )對.
A. 0 B.1 C.2 D.3
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省韶關市高三4月高考模擬(二模)文科數學試卷(解析版) 題型:選擇題
執行如圖所示的程序框圖,若輸出的結果是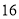 ,則判斷框內的條件( )
,則判斷框內的條件( )
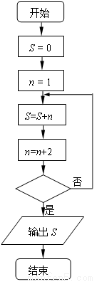
A.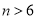 ? B.
? B.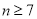 ? C.
? C.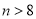 ? D.
? D.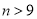 ?
?
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省肇慶市高三3月第一次模擬理科數學試卷(解析版) 題型:解答題
已知向量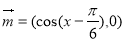 ,
,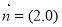 ,
, ,函數
,函數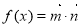 .
.
(1)求函數 的表達式;
的表達式;
(2)求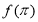 的值;
的值;
(3)若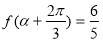 ,
, ,求
,求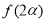 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com