
分析 利用復數代數形式的乘除運算化簡復數z,然后代入ω=z+ai,再求出$\frac{ω}{z}$,由復數求模公式求出$|\frac{ω}{z}|$,求解一元二次不等式可得答案.
解答 解:$z=\frac{(-1+3i)(1-i)-(1+3i)}{i}=\frac{(2+4i)-(1+3i)}{i}=\frac{1+i}{i}=1-i$,
∵ω=z+ai=1-i+ai=1+(a-1)i,
∴$\frac{ω}{Z}=\frac{1+(a-1)i}{1-i}=\frac{[1+(a-1)i](1+i)}{2}=\frac{2-a+ai}{2}$.
∴$|\frac{ω}{z}|=\frac{{\sqrt{{{(2-a)}^2}+{a^2}}}}{2}≤\sqrt{2}$,
∴a2-2a-2≤0,
解得$1-\sqrt{3}≤a≤1+\sqrt{3}$.
故a的取值范圍是[$1-\sqrt{3},1+\sqrt{3}$].
點評 本題考查了復數代數形式的混合運算,考查了復數模的求法以及一元二次不等式的解法,是基礎題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 圓 | B. | 橢圓 | C. | 雙曲線 | D. | 拋物線 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 如圖,曲線C1是橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一部分,F1,F2是其兩焦點.曲線C2是以原點O為頂點、F2為焦點的拋物線的一部分,A是曲線C1和C2的一個公共點,并且∠AF2F1為鈍角.我們把由曲線C1和C2合成的曲線C稱為“月食圓”.
如圖,曲線C1是橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一部分,F1,F2是其兩焦點.曲線C2是以原點O為頂點、F2為焦點的拋物線的一部分,A是曲線C1和C2的一個公共點,并且∠AF2F1為鈍角.我們把由曲線C1和C2合成的曲線C稱為“月食圓”.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
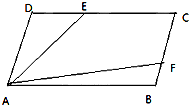 在平行四邊形ABCD中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,E、F分別是邊CD和BC上的點,滿足$\overrightarrow{DC}$=3$\overrightarrow{DE}$,$\overrightarrow{BC}$=3$\overrightarrow{BF}$.
在平行四邊形ABCD中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,E、F分別是邊CD和BC上的點,滿足$\overrightarrow{DC}$=3$\overrightarrow{DE}$,$\overrightarrow{BC}$=3$\overrightarrow{BF}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|0≤x≤1} | B. | {x|1≤x<2} | C. | {x|-1<x≤0} | D. | {x|0≤x<1} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
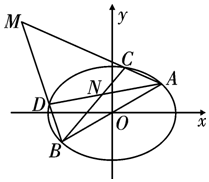 如圖,已知橢圓C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),點A($\sqrt{2}$,1)是橢圓上的一點,且橢圓C的離心率為$\frac{{\sqrt{2}}}{2}$,直線AO與橢圓C交于點B,且C,D是橢圓上異于A,B的任意兩點,直線AC,BD相交于點M,直線AD,BC相交于點N.
如圖,已知橢圓C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),點A($\sqrt{2}$,1)是橢圓上的一點,且橢圓C的離心率為$\frac{{\sqrt{2}}}{2}$,直線AO與橢圓C交于點B,且C,D是橢圓上異于A,B的任意兩點,直線AC,BD相交于點M,直線AD,BC相交于點N.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com