
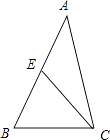
【題目】在△ABC中,a,b,c分別為A,B,C所對邊,a+b=4,(2﹣cosA)tan ![]() =sinA.
=sinA.
(1)求邊長c的值;
(2)若E為AB的中點,求線段EC的范圍.
【答案】
(1)解:在△ABC中,∵(2﹣cosA)tan ![]() =sinA,a+b=4,
=sinA,a+b=4,
∴(2﹣cosA) ![]() =sinA,
=sinA,
即2sinC=sinA+sinAcosC+cosAsinC=sinA+sinB,
∴由正弦定理可得:2c=a+b=4,
∴c=2.
(2)解:∵c=2,E為AB的中點,
∴由余弦定理可得:CE2=AE2+AC2﹣2AEACcosA=a2+1﹣2acosB,
CE2=BE2+BC2﹣2BEBCcosB=b2+1﹣2bcosA,
∴兩式相加可得:CE2= ![]() ,
,
又∵cosB= ![]() ,cosA=
,cosA= ![]() ,a=4﹣b,
,a=4﹣b,
∴ ![]() ,
,
又∵ ![]() ,
,
∴1<b<3,
∴ ![]() .
.
【解析】(1)使用半角公式化簡條件式,利用正弦定理結合已知即可得解c的值.(2)利用已知及余弦定理可得 ![]() ,又結合
,又結合 ![]() ,可得b的范圍,利用二次函數的性質即可解得CE的范圍.
,可得b的范圍,利用二次函數的性質即可解得CE的范圍.


科目:高中數學 來源: 題型:
【題目】如圖,正方形ABCD邊長為2,以D為圓心、DA為半徑的圓弧與以BC為直徑的半圓O交于點F,連結CF并延長交AB于點E. 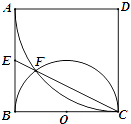
(1)求證:AE=EB;
(2)求EFFC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
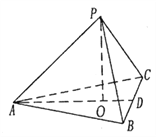
【題目】在三棱錐![]() 中,
中, ![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() 平面
平面![]() ,垂足
,垂足![]() 落在線段
落在線段![]() 上,已知
上,已知![]() .
.
(1)證明: ![]() ;
;
(2)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得二面角
,使得二面角![]() 為直二面角?若存在,求出
為直二面角?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是實數,已知奇函數
是實數,已知奇函數![]() ,
,
(1)求![]() 的值;
的值;
(2)證明函數![]() 在R上是增函數;
在R上是增函數;
(3)若對任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0有解,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,過點
,過點![]() 的直線與橢圓
的直線與橢圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() 的周長為8.
的周長為8.
(1)求橢圓![]() 的方程;
的方程;
(2)若經過原點![]() 的直線與橢圓
的直線與橢圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,試判斷
,試判斷![]() 是否為定值?若為定值,試求出該定值;否則,請說明理由.
是否為定值?若為定值,試求出該定值;否則,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體![]() 中,四邊形
中,四邊形![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,四邊形
,四邊形![]() 為矩形.
為矩形.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)線段![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ?若存在,確定點
?若存在,確定點![]() 的位置并加以證明.
的位置并加以證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com