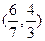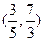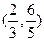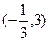(本大題共15分)已知
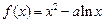
在
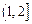
上是增函數(shù),
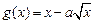
在
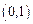
上是減函數(shù).(1)求
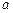
的值;(2)設函數(shù)
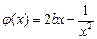
在
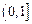
上是增函數(shù),且對于
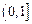
內的任意兩個變量
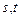
,恒有
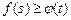
成立,求實數(shù)
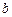
的取值范圍;(3)設
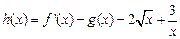
,求證:
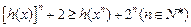
.
:(1)
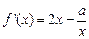
,依題意,當
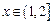
時,
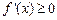
恒成立,即
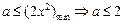
.
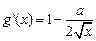
,當
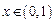
時,
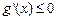
恒成立,即
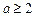
,所以
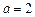
.…………5分
(2)
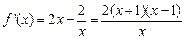
,所以

在
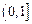
上是減函數(shù),最小值是
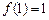
.
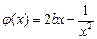
在
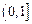
上是增函數(shù),即
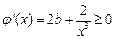
恒成立,得
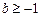
,且
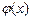
的最大值是
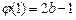
,由已知得
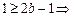
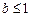
,所以
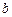
的取值范圍是
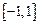
.…………5分
(3)

,
方法一:
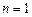
時不等式左右相等,得證;
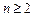
時,
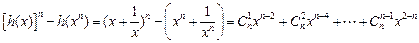
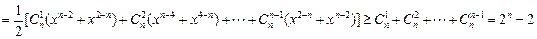
,
所以
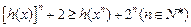
成立. ……5分
方法二:
用數(shù)學歸納法很快可證,方法很好.證明略.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知:三次函數(shù)
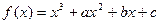
,在
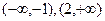
上單調增,在(-1,2)上單調減,當且僅當
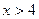
時,
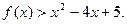
(1)求函數(shù)
f (
x)的解析式; (2)若函數(shù)
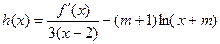
,求
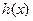
的單調區(qū)間.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
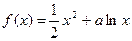
(a∈R).(1)若
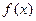
在[1,e]上是增函數(shù),求a的取值范圍(2)若a=1,a≤x≤e,證明:
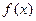
<
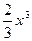
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設函數(shù)
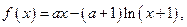
其中
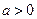
。(1)求
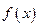
的單調區(qū)間;
(2)當
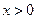
時,證明不等式:
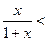
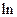
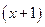
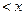
;
(3)設
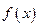
的最小值為
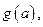
證明不等式:
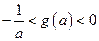
。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)
已知函數(shù)
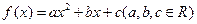
,當
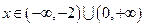
時,
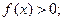
當
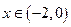
時,
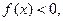
且對任意
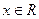
不等式
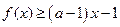
恒成立.
1)求函數(shù)
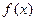
的解析式;
2)設函數(shù)
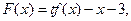
其中
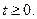
求
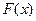
在
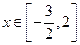
時的最大值
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)已知函數(shù)
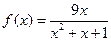
(
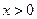
) , (Ⅰ)試確定
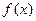
的單調區(qū)間 , 并證明你的結論 ;(Ⅱ)若
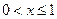
時 , 不等式
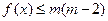
恒成立 , 求實數(shù)
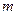
的取值范圍 .
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知函數(shù)
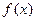
的定義域為[—2,
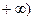
,部分對應值如下表。
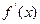
為
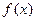
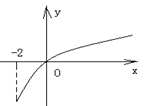
的導函數(shù),函數(shù)
的圖象如右圖所示:
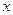
| —2
| 0
| 4
|
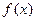
| 1
| —1
| 1
|
若兩正數(shù)
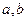
滿足
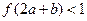
,則
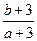
的取值范圍是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
函數(shù)y=
sinx的導數(shù)為( )
| A.y′=2sinx+cosx | B.y′=-cosx |
| C.y′=+cosx | D.y′=+cosx |
查看答案和解析>>

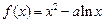 在
在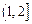 上是增函數(shù),
上是增函數(shù),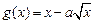 在
在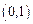 上是減函數(shù).(1)求
上是減函數(shù).(1)求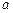 的值;(2)設函數(shù)
的值;(2)設函數(shù)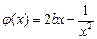 在
在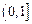 上是增函數(shù),且對于
上是增函數(shù),且對于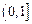 內的任意兩個變量
內的任意兩個變量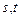 ,恒有
,恒有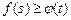 成立,求實數(shù)
成立,求實數(shù)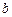 的取值范圍;(3)設
的取值范圍;(3)設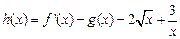 ,求證:
,求證: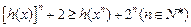 .
.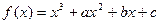 ,在
,在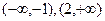 上單調增,在(-1,2)上單調減,當且僅當
上單調增,在(-1,2)上單調減,當且僅當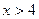 時,
時,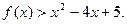
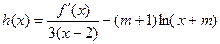 ,求
,求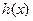 的單調區(qū)間.
的單調區(qū)間.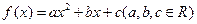 ,當
,當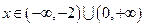 時,
時,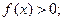 當
當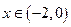 時,
時,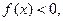 且對任意
且對任意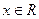 不等式
不等式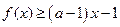 恒成立.
恒成立.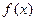 的解析式;
的解析式;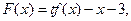 其中
其中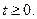 求
求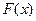 在
在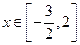 時的最大值
時的最大值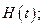
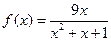 (
(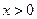 ) , (Ⅰ)試確定
) , (Ⅰ)試確定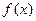 的單調區(qū)間 , 并證明你的結論 ;(Ⅱ)若
的單調區(qū)間 , 并證明你的結論 ;(Ⅱ)若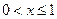 時 , 不等式
時 , 不等式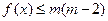 恒成立 , 求實數(shù)
恒成立 , 求實數(shù)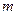 的取值范圍 .
的取值范圍 . 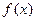 的定義域為[—2,
的定義域為[—2,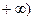 ,部分對應值如下表。
,部分對應值如下表。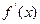 為
為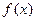 的導函數(shù),函數(shù)
的導函數(shù),函數(shù)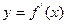 的圖象如右圖所示:
的圖象如右圖所示:
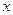
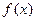
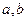 滿足
滿足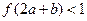 ,則
,則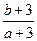 的取值范圍是( )
的取值范圍是( )